Let $$\triangle ABC$$ be a triangle right-angled at B with AB = BC = 18. The area of the largest rectangle that can be inscribed in this triangle and has B as one of the vertices is:
Correct Answer: 81
Solution
ABC is a right angled triangle at B, and said that rectangle has to inscribed inside with B as one of its vertices :
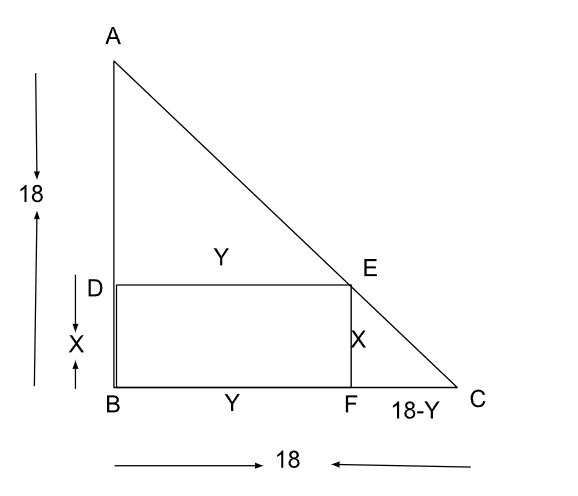
As triangle ABC and EFC are similar , we can say that : $$\dfrac{\ AB}{BC}=\ \dfrac{\ EF}{FC}$$
$$\dfrac{\ 18}{18}=\ \dfrac{\ X}{18-Y}$$
This implies X+Y = 18.
Area of rectangle is X(Y) = X(18-X) = $$18X-X^2$$
This will be maximum at X = 18/2 = 9
Therefore largest area is 9x9 = 81.
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

