The number of pairs (x, y) of integers satisfying the inequality $$\mid x - 5 \mid + \mid y - 5 \mid \leq 6$$ is:
Correct Answer: 85
Solution
Lets assume |X-5| = a & |Y-5| = b :
$$\left|a\right|\ +\ \left|b\right|\ \le\ 6$$
The graph with horizontal axis as "a" & vertical axis "b" will look like :
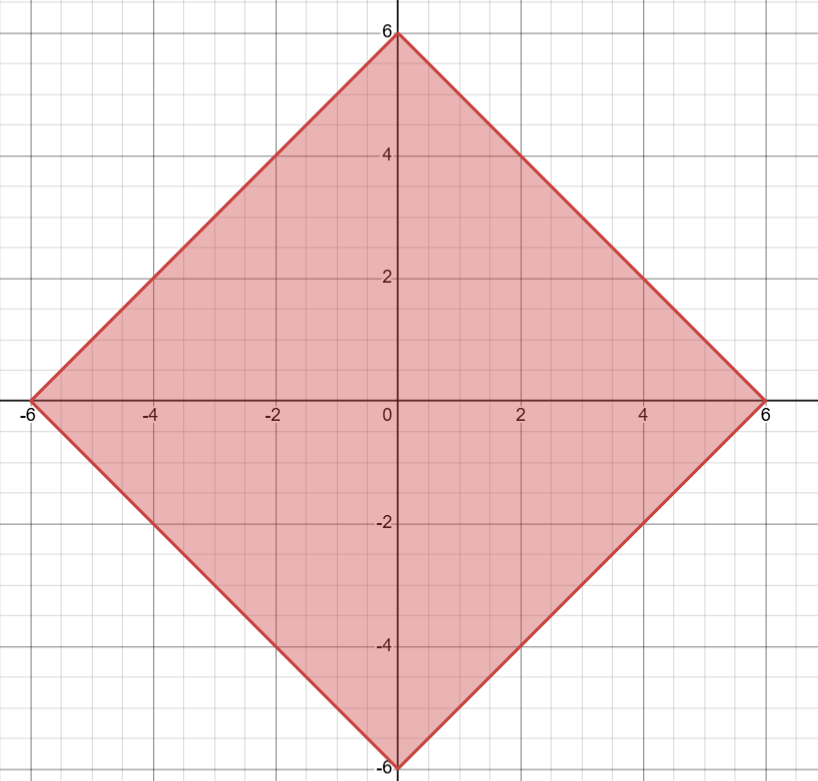
The points which satisfy this inequality will be (a,b) :
Case I : Points on the line/boundary :
(0,$$\pm6$$) (1,$$\pm5$$) (2,$$\pm4$$) (3,$$\pm3$$) (4,$$\pm2$$) (5,$$\pm1$$) (6,0)
(-1,$$\pm5$$) (-2,$$\pm4$$) (-3,$$\pm3$$) (-4,$$\pm2$$) (-5,$$\pm1$$) (-6,0)
Therefore , on the boundary = 24
Case II : Points which lie inside the boundary :
(0,0)
($$\pm1$$,0) ($$\pm2$$,0) ($$\pm3$$,0), ($$\pm4$$,0) ,($$\pm5$$,0)
(0,$$\pm1$$) (0,$$\pm2$$) (0,$$\pm3$$), (0,$$\pm4$$) ,(0,$$\pm5$$)
For X = $$\pm1$$ : 2x2x4 = 16
For X = $$\pm2$$ : 2x2x3 = 12
For X = $$\pm3$$ : 2x2x2 = 8
For X = $$\pm4$$ : 2x2x1 = 4
Therefore , inside no of points = 1+10+10+16+12+8+4 = 61
Hence total no of integral points which satisfy the inequality will be = 61+24 = 85.
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

