The following table shows the number of employees and their median age in eight companies located in a district.

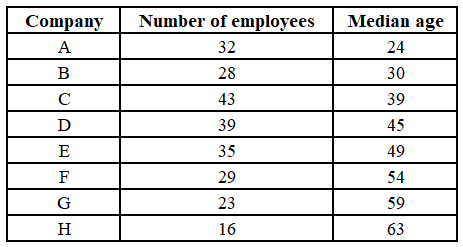
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C, ..., the age of every employee in G is strictly less than the age of every employee in H.

In company F, the lowest possible sum of the ages of all employees is:

F has 29 employees. So the median will be the age of the 15th employee, which is 54. E has 35 employees, so the median will be the age of the 18th employee, which is 49.

We need to find the minimum possible sum of the ages of all the employees of F.

For that, we also need to minimise the highest possible age in E, as no employee in E is older than the employees in F. 

Now, the median age of E is 49, which would mean that if at least 18 people in E are aged 49, the remaining aged below 49, then too, the median will be 49. This would mean that the minimum possible age in Company F is 50. 

Also, since the median age in F is 54, at least 15 employees should be aged 54 for the median to hold true. 

So the minimum age will be when 15 employees are aged 54 and the remaining 14 employees are aged 50, the minimum sum of ages being 50x14+54x15 = 1510.