IPM Indore 2024 Question Paper
For the following questions answer them individually
IPM Indore 2024 - Question 11
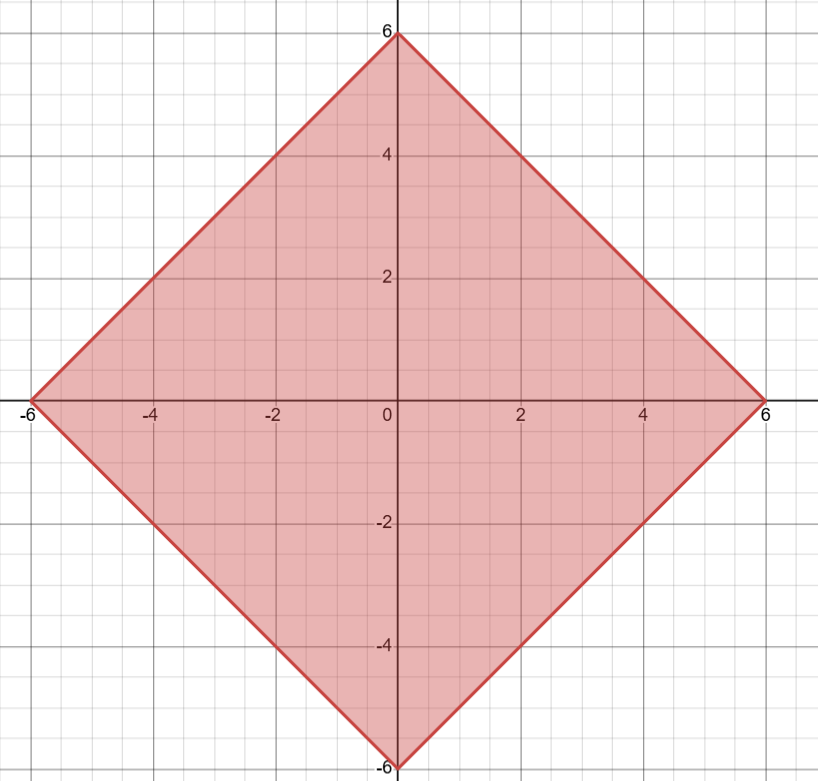
The number of pairs (x, y) of integers satisfying the inequality $$\mid x - 5 \mid + \mid y - 5 \mid \leq 6$$ is:
789
456
123
0.-
Clear All
IPM Indore 2024 - Question 12
The following table shows the number of employees and their median age in eight companies located in a district.
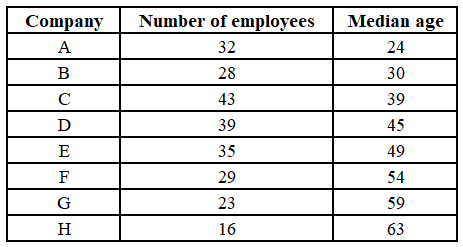
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C, ..., the age of every employee in G is strictly less than the age of every employee in H.
In company F, the lowest possible sum of the ages of all employees is:
789
456
123
0.-
Clear All
IPM Indore 2024 - Question 13
In a group of 150 students, 52 like tea, 48 like juice and 62 like coffee. If each student in the group likes at least one among tea, juice and coffee, then the maximum number of students that like more than one drink is:
789
456
123
0.-
Clear All
IPM Indore 2024 - Question 14
The price of a chocolate is increased by x% and then reduced by x%. The new price is 96.76% of the original price. Then x is:
789
456
123
0.-
Clear All
IPM Indore 2024 - Question 15
Let f and g be two functions defined by $$f(x) = \mid x + \mid x \mid \mid$$ and $$g(x) = \frac{1}{x}$$ for $$x \neq 0$$. If $$f(a) + g(f(a)) = \frac{13}{6}$$ for some real a, then the maximum possible value of $$f(g(a))$$ is:
789
456
123
0.-
Clear All
IPM Indore 2024 - Question 16
The terms of a geometric progression are real and positive. If the p-th term of the progression is q and the q-th term is p, then the logarithm of the first term is
IPM Indore 2024 - Question 17
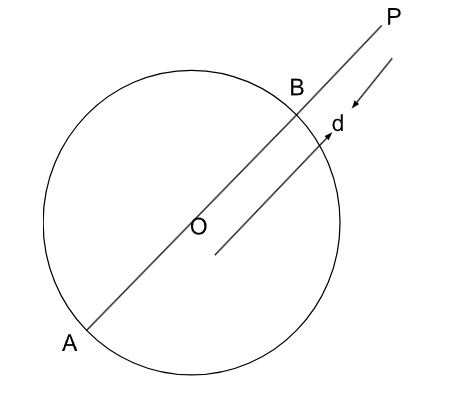
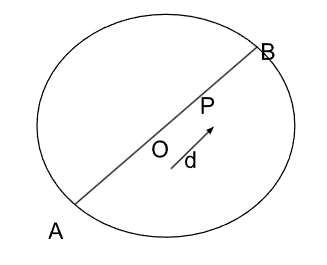
If the shortest distance of a given point to a given circle is 4 cm and the longest distance is 9 cm, then the radius of the circle is
IPM Indore 2024 - Question 18
If $$\mid x + 1 \mid + (y + 2)^2 = 0$$ and $$ax - 3ay = 1$$, Then the value of a is
IPM Indore 2024 - Question 19
The number of real solutions of the equation $$x^2 - 10 \mid x \mid - 56 = 0$$ is
IPM Indore 2024 - Question 20
The greatest number among $$2^{300}, 3^{200}, 4^{100}, 2^{100} + 3^{100}$$ is