IPM Indore 2024 Question Paper
For the following questions answer them individually
IPM Indore 2024 - Question 21
The sum of a given infinite geometric progression is 80 and the sum of its first two terms is 35. Then the value of n for which the sum of its first n terms is closest to 100, is
IPM Indore 2024 - Question 22
Let $$n$$ be the number of ways in which $$20$$ identical balloons can be distributed among $$5$$ girls and $$3$$ boys such that everyone gets at least one balloon and no girl gets fewer balloons than a boy does. Then
IPM Indore 2024 - Question 23
Let $$a = \dfrac{(\log_7 4)(\log_7 5 - \log_7 2)}{\log_7 25(\log_7 8 - \log_7 4)}$$. Then the value of $$5^a$$ is
IPM Indore 2024 - Question 24
The smallest possible number of students in a class if the girls in the class are less than 50% but more than 48% is
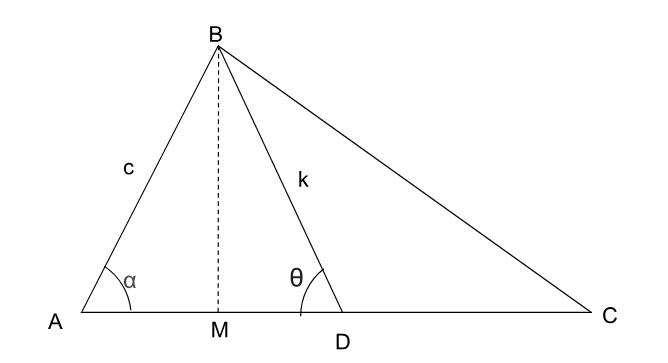
IPM Indore 2024 - Question 25
The side AB of a triangle ABC is c. The median BD is of length k. If $$\angle BDA = \theta$$ and $$\theta < 90^\circ$$, then the area of triangle ABC is
IPM Indore 2024 - Question 26
Let $$\triangle ABC$$ be a triangle with $$AB = AC$$ and $$D$$ be a point on $$BC$$ such that $$\angle BAD = 30^\circ$$. If E is a point on $$AC$$ such that $$AD = AE$$, then $$\angle CDE$$ equals
IPM Indore 2024 - Question 27
If $$\log_4 x = a$$ and $$\log_{25} x = b$$, then $$\log_x 10$$ is
IPM Indore 2024 - Question 28
If 5 boys and 3 girls sit randomly around a circular table, the probability that there will be at least one boy sitting between any two girls is
IPM Indore 2024 - Question 29
A fruit seller had a certain number of apples, bananas, and oranges at the start of the day. The number of bananas was 10 more than the number of apples, and the total number of bananas and apples was a multiple of 11. She was able to sell 70% of the apples, 60% of bananas, and 50% of oranges during the day. If she was able to sell 55% of the fruits she had at the start of the day, then the minimum number of oranges she had at the start of the day was
IPM Indore 2024 - Question 30
A boat goes 96 km upstream in 8 hours and covers the same distance moving downstream in 6 hours. On the next day it starts from point A, goes downstream for 1 hour, then upstream for 1 hour, and repeats this for four more times, that is, 5 upstream and 5 downstream journeys. Then the boat would be
.jpg)

