IPM Indore 2024 Question Paper

The number of solutions of the equation $$x_1 + x_2 + x_3 + x_4 = 50$$, where $$x_1 , x_2 , x_3 , x_4$$ are integers with $$x_1 \geq1, x_2 \geq 2, x_3 \geq 0, x_4 \geq 0$$ is

The numbers $$2^{2024}$$ and $$5^{2024}$$ are expanded and their digits are written out consecutively on one page. The total number of digits written on the page is

If $$\theta$$ is the angle between the pair of tangents drawn from the point $$\left(0, \frac{7}{2}\right)$$ to the circle $$x^2 + y^2 - 14x + 16y + 88 = 0$$, then $$\tan \theta$$ equals

The difference between the maximum real root and the minimum real root of the equation $$(x^2 - 5)^4 + (x^2 - 7)^4 = 16$$ is

The angle of elevation of the top of a pole from a point A on the ground is $$30^\circ$$. The angle of elevation changes to $$45^\circ$$, after moving 20 meters towards the base of the pole. Then the height of the pole, in meters, is

The number of values of x for which $$C\left(\begin{array}{c}17-x\\ 3x + 1\end{array}\right)$$ is defined as an integer is

Let ABC be an equilateral triangle, with each side of length . If a circle is drawn with diameter AB, then the area of the portion of the triangle lying inside the circle is

Sagarika divides her savings of 10000 rupees to invest across two schemes A and B. Scheme A offers an interest rate of 10% per annum, compounded half-yearly, while scheme B offers a simple interest rate of 12% per annum. If at the end of first year, the value of her investment in scheme B exceeds the value of her investment in scheme A by 2310 rupees, then the total interest, in rupees, earned by Sagarika during the first year of investment is

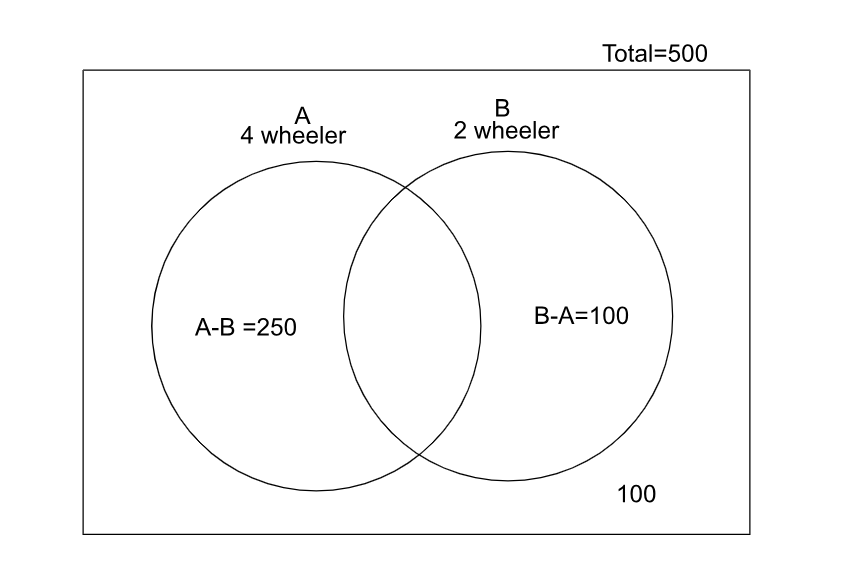
In a survey of 500 people, it was found that 250 owned a 4-wheeler but not a 2- wheeler, 100 owned a 2-wheeler but not a 4-wheeler, and 100 owned neither a 4- wheeler nor a 2-wheeler. Then the number of people who owned both is

For some non-zero real values of $$a, b$$ and $$c$$, it is given that $$\mid \frac{c}{a} \mid = 4, \mid \frac{a}{b} \mid = \frac{1}{3}$$ and $$\frac{b}{c} = -\frac{3}{4}$$. If $$ac > 0$$, then $$\left(\frac{b + c}{a}\right)$$