In a survey of 500 people, it was found that 250 owned a 4-wheeler but not a 2- wheeler, 100 owned a 2-wheeler but not a 4-wheeler, and 100 owned neither a 4- wheeler nor a 2-wheeler. Then the number of people who owned both is

The situation is best represented using a Venn diagram. Here, let A denote the set of people who own a 4-wheeler, and B denote the set of people who own a 2-wheeler. Then the number of people who own a 4-wheeler but not a 2-wheeler is A-B, which is igvwn to be 250. And the number of people who own a two-wheeler but not a 4-wheeler is B-A=100 , the number of people who own none is 100, and the total number of people in the survey is 500. We have to find the number of people who own both a 2-wheeler and a 4-wheeler., which is $$A\cap B$$

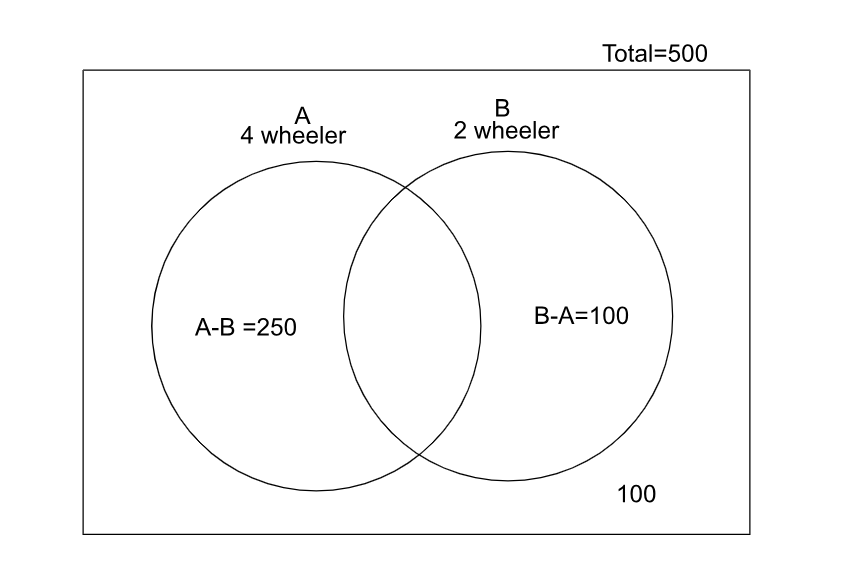
Total number of people who own at least one of either a 2-wheeler or a 4-wheeler is $$A\cup B$$ which is total - number of people who own none =500-100=400.

Now, $$n\left(A\cup B\right)=n\left(A-B\right)+n\left(A\cap B\right)+n\left(B-A\right)$$

So, $$400=250+n\left(A\cap B\right)+100$$

or, $$n\left(A\cap B\right)=400-250-100=50$$ 

Hence, the number of people who own both is 50.