The side AB of a triangle ABC is c. The median BD is of length k. If $$\angle BDA = \theta$$ and $$\theta < 90^\circ$$, then the area of triangle ABC is
Solution
Based on the information given in the question, a diagram is constructed where BM is the median of AC. Since the question deals with areas, we construct BM as the altitude for the triangle. $$\angle\ BDA=\theta\ $$ (given) and $$\angle\ BAD=\alpha\ $$ is assumed. The following figure is obtained.
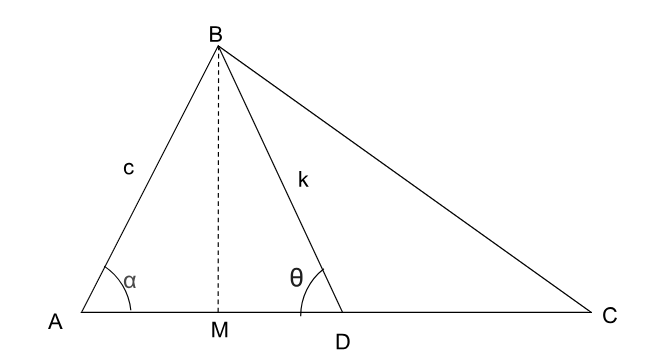
BM is the height, and so $$\angle\ BMA=\angle\ BMD=90^{\circ\ }$$
So, in $$\triangle\ BAM$$,
$$\sin\alpha\ =\frac{BM}{AB}=>\ BM=c\ \sin\alpha\ $$
$$\cos\ \alpha\ =\frac{AM}{AB}=>AM=c\cos\alpha\ $$
Again, in $$\triangle\ BDM$$,
$$\sin\theta\ =\frac{BM}{BD}=>\ BM=k\ \sin\theta\ $$
$$\cos\ \theta\ =\frac{DM}{BD}=>DM=k\cos\theta\ $$
Now, area of $$\triangle\ ABD$$ can be calculated as $$\dfrac{1}{2}\times\ AD\times\ BM=\frac{1}{2}\times\ \left(AM+BM\right)\times\ BM$$
Putting the values obtained we have,
$$ar\triangle\ ABD=\frac{1}{2}\times\ \left(c\ \cos\alpha\ +k\ \cos\theta\ \right)\times\ k\ \sin\theta\ $$ ________(A)
Now, $$c\ \sin a=\ k\ \sin\theta\ =>\sin\ \alpha\ =\dfrac{k\sin\theta\ }{c}\ $$
So, $$\cos\ \alpha\ =\sqrt{\ 1-\left(\frac{k\sin\theta\ }{c}\ \right)^2}=\dfrac{\sqrt{\ c^2-k^2\sin^2\theta\ }}{c}$$
Substituting this in (A) we have
$$ar\triangle\ ABD=\frac{1}{2}\times\ \left(\sqrt{\ c^2-k^2\sin^2\theta\ }\ +k\ \cos\theta\ \right)\times\ k\ \sin\theta\ $$
or, $$ar\triangle\ ABD=\frac{1}{2}\left(\ k\sin\theta\ \sqrt{c^2-k^2\sin^2\theta\ }\ +k^2\ \cos\theta\sin\theta\ \right)$$
or, $$ar\triangle\ ABD=\frac{1}{2}\left(\ k\sin\theta\ \sqrt{c^2-k^2\sin^2\theta\ }\ +\frac{k^2}{2}\times\ \ 2\cos\theta\sin\theta\ \right)$$
or, $$ar\triangle\ ABD=\dfrac{1}{2}\left(\ k\sin\theta\ \sqrt{c^2-k^2\sin^2\theta\ }\ +\dfrac{k^2}{2}\sin2\theta\ \right)$$
Now, since BD is the median, this means the area of $$ar\triangle\ ABC=2\ ar\triangle\ ABD$$
so , $$ar\triangle\ ABC=\ k\sin\theta\ \sqrt{c^2-k^2\sin^2\theta\ }\ +\dfrac{k^2}{2}\sin2\theta\ $$ , which is option B.
Create a FREE account and get:
- Download Maths Shortcuts PDF
- Get 300+ previous papers with solutions PDF
- 500+ Online Tests for Free

