The following table shows the number of employees and their median age in eight companies located in a district.

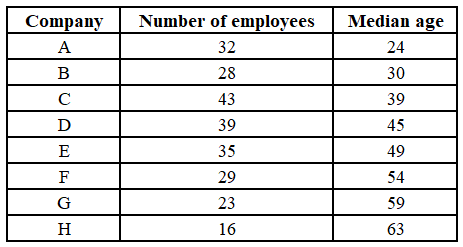
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C, ..., the age of every employee in G is strictly less than the age of every employee in H. The highest possible age of an employee of company A is:

Here, we are told that the number of employees in company A is 32 and their median age is 24; and the number of employees in company B is 28 and their median age is 30 years. 

Median age here refers to the middle value . As in for the 28 employees in company B, when arranged in ascending order, mean of the ages of the 14th and 15th employees is 30. Similarly , in case of company A , the median age is 24. We are also told that the age of every employee of company A is strictly less than that of every employee in company B. 

In a case where 15 employees ($$\left(\frac{28}{2}+1\right)$$ in company B are aged 30, no matter what the age of the remaining 13 employees is, the median age of the company becomes 30. In that case the maximum age for an employee in company A can be 29. 

The age for an employee in A cannot be more than 29, as in that case the rule that age of all employees in A is strictly less than that in B will be violated. If even one person in company A is aged 30, all the employees in company B must be older than 30, and therefore the median age for company B can never be 30.

Hence, the highest possible age of an employee of company A is 29 years.