IPM Indore 2022 Question Paper

The number of triangles that can be formed by choosing points from 7 points on a line and 5 points on another parallel line is_________.

A new sequence is obtained from the sequence of positive integers (1, 2, 3,...) by deleting all the perfect squares. Then the $$2022^{nd}$$ term of the new sequence is___________.

When Geeta increases her speed from 12 km/hr to 20 km/hr, she takes one hour less than the usual time to cover the distance between her home and office. The distance between her home and office is________km.

The $$3^{rd}, 14^{th}$$ and $$69^{th}$$ terms of an arithmetic progression form three distinct and consecutive terms of a geometric progression. If the next terms of the geometries progression is the $$n^{th}$$ term of the arithmetic progression, then n quals____________.

Given that
$$f(x)=|x|+2|x−1|+|x−2|+|x−4|+|x−6|+2|x−10|$$, $$x \epsilon (-\infty, \infty)$$
the minimum value of f(x) is _________.

The sum of the first 15 terms in an arithmetic progression in 200, while the sum of the next 15 terms in 350, then the common difference is

For $$0 < \theta < \frac{\pi}{4}$$, let
$$a = ((\sin \theta)^{\sin \theta}) (\log_{2} \cos \theta)$$, $$b = ((\cos \theta)^{\sin \theta}) (\log_{2} \sin \theta)$$
$$c = ((\sin \theta)^{\cos \theta}) (\log_{2} \cos \theta)$$ and $$d = ((\sin \theta)^{\sin \theta}) (\log_{2} \sin \theta)$$
Then, the median value in the sequence a, b, c, d is

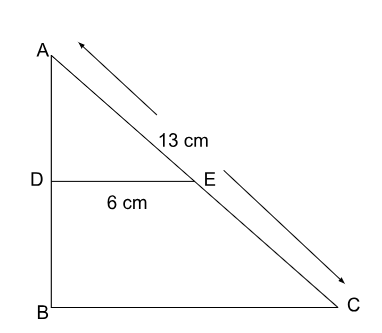
In a right-angled triangle ABC, the hypotenuse AC is of length 13 cm. A line drawn connecting the midpoints D and E of sides AB and AC is found to be 6 cm in length. The length of BC is

In a room, there are n persons whose average height is 160 cm. If m more persons, whose average height is 172 cm, enter the room, then the average height of all persons in the room becomes 164 cm. Then m : n is

The number of four-digit integers which are greater than 1000 and divisible by both 2 and 3, but not by 5, is