The number of triangles that can be formed by choosing points from 7 points on a line and 5 points on another parallel line is_________.

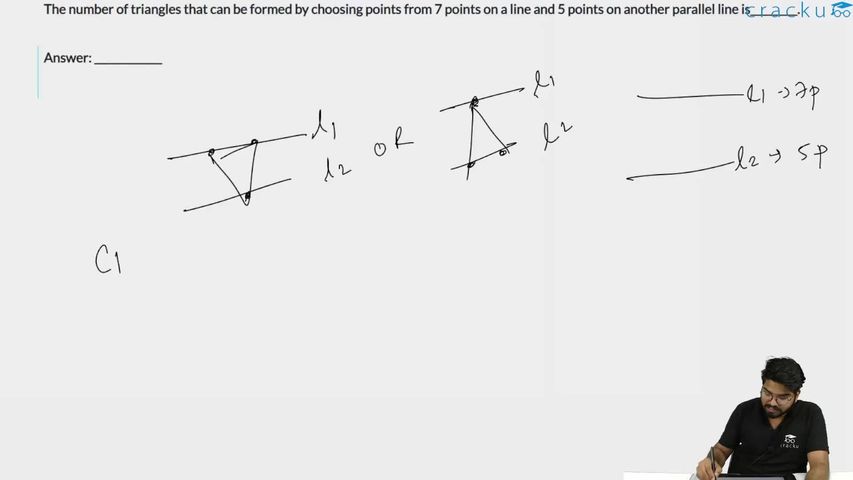
Let, the line having 7 points be denoted as L1 and the line having 5 points be denoted as L2

A triangle is formed by 3 points (not all collinear)

In this case, in 2 ways a traingle can be formed.

i.) One point is at L1 and the other two points are at L2:

Number of ways of choosing one point in L1 is $$^7C_1$$ and, number of ways of choosing two points in L2 is $$^5C_2$$

So, number of triangles in this case = $$^7C_1\cdot^5C_2=7\times\ \dfrac{5\times\ 4}{2}=7\times\ 5\times\ 2=70$$

ii.) One point is at L2 and the other two points are at L1:

Number of ways of choosing one point in L2 is $$^5C_1$$ and, number of ways of choosing two points in L1 is $$^7C_2$$

So, number of triangles in this case = $$^5C_1\cdot^7C_2=5\times\ \dfrac{7\times\ 6}{2}=5\times\ 7\times\ 3=105$$

So, total number of triangles = $$70+105=175$$