Please enter the following details
A triangle ABC has area 32 sq units and its side BC, of length 8 units, lies on the line x = 4. Then the shortest possible distance between A and the point (0,0) is
We know that area of the triangle = 32 sq. units, BC = 8 units
Therefore, the height of the perpendicular drawn from point A to BC = 2*32/8 = 8 units.
Let us draw a possible diagram of the given triangle.
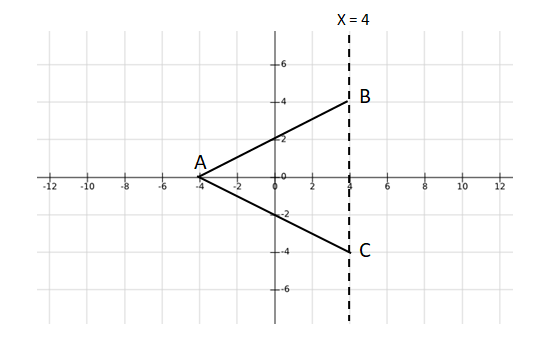
We can see that if A coincide with (-4, 0) then the distance between A and (0, 0) = 4 units.
If we move the triangle up or down keeping the base BC on x = 4, then point A will move away from origin as vertical distance will come into factor whereas horizontal distance will remain as 4 units.
Hence, we can say that minimum distance between A and origin (0, 0) = 4 units.
Video Solution
Your Doubts
Drop Your File Here!
Ask Your Doubt
Drop Your File Here!
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
