Join WhatsApp Icon CAT WhatsApp Group
Question 86

On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is


Correct Answer: 24

Solution

Share

Let us draw the diagram according to the available information.

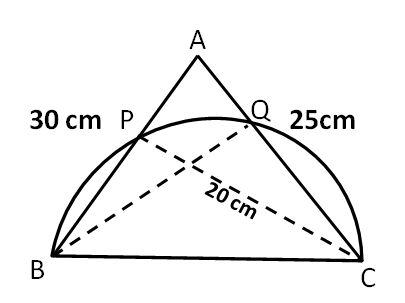
We can see that triangle BPC and BQC are inscribed inside a semicircle. Hence, we can say that

$$\angle$$ BPC = $$\angle$$ BQC = 90°

Therefore, we can say that BQ  $$\perp$$ AC and CP $$\perp$$ AB.

In triangle ABC,

Area of triangle = (1/2)*Base*Height = (1/2)*AB*CP = (1/2)*AC*BQ

$$\Rightarrow$$ BQ = $$\dfrac{AB*CP}{AC}$$ = $$\dfrac{30*20}{25}$$ = 24 cm.

Was this solution helpful?

Get AI Help

Video Solution

video
View More Questions From Geometry

Create a FREE account and get:

  • All Quant CAT complete Formulas and shortcuts PDF
  • 41+ CAT previous year papers with video solutions PDF
  • 5000+ Topic-wise Previous year CAT Solved Questions for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Coordinate Geometry QuestionsCAT Inequalities QuestionsCAT Number Series QuestionsCAT Time Speed Distance QuestionsCAT Averages Mixtures Alligations Questions

CAT DILR Questions | LRDI Questions For CAT

CAT Games and Tournaments QuestionsCAT Special Charts QuestionsCAT Selection With Condition QuestionsCAT Data change over a period QuestionsCAT Coins and Weights Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Odd One Out QuestionsCAT Reading Comprehension QuestionsCAT Critical Reasoning QuestionsCAT Vocabulary QuestionsCAT Grammar and Sentence Correction Questions

Free CAT Quant Questions

CAT Quadratic EquationsCAT GeometryCAT Linear EquationsCAT MiscellaneousCAT MensurationCAT Averages, Ratio and ProportionCAT Coordinate GeometryCAT Profit And LossCAT Time, Speed and DistanceCAT Probability, CombinatoricsCAT Simple Interest Compound InterestCAT Venn DiagramsCAT AveragesCAT Functions, Graphs and StatisticsCAT Number SystemsCAT PercentagesCAT ArithmeticCAT AlgebraCAT Logarithms, Surds and IndicesCAT Progressions and SeriesCAT Averages Mixtures AlligationsCAT Time And WorkCAT Number SeriesCAT LogarithmsCAT InequalitiesCAT Data SufficiencyCAT Profit and LossCAT Time Speed DistanceCAT Remainders

Related Formulas With Tests

Angles subtended on a circle Triangles - Area

Book Free CAT Mentorship

Get personalized CAT strategy from a 99%iler

500+ students mentored
CAT mentor

Join CAT 2026 course by 5-Time CAT 100%iler

Start your IIM journey with the right preparation and crack CAT 2026.

Enroll Now
Ask AI