Sign in
Please select an account to continue using cracku.in
↓ →
From a rectangle ABCD of area 768 sq cm, a semicircular part with diameter AB and area 72π sq cm is removed. The perimeter of the leftover portion, in cm, is
Area of the semicircle with AB as a diameter = $$\dfrac{1}{2}*\pi*(\dfrac{AB^2}{4})$$
$$\Rightarrow$$ $$\dfrac{1}{2}*\pi*(\dfrac{AB^2}{4})$$ = $$72*\pi$$
$$\Rightarrow$$ $$AB = 24 cm$$
Given that area of the rectangle ABCD = 768 sq.cm
$$\Rightarrow$$ AB*BC = 768
$$\Rightarrow$$ BC = 32 cm
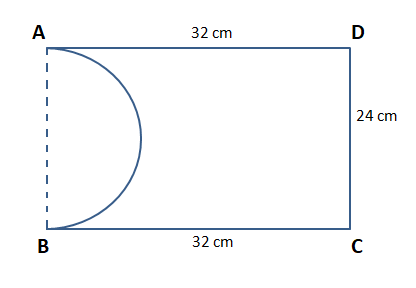
We can see that the perimeter of the remaining shape = AD + DC + BC + Arc(AB)
$$\Rightarrow$$ 32+24+32+$$\pi*24/2$$
$$\Rightarrow$$ $$88+12\pi$$

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation