CAT Content

CAT 2017 Question Paper (Shift-2) Question 84
Question 84

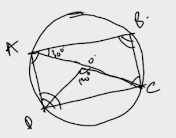
ABCD is a quadrilateral inscribed in a circle with centre O such that O lies inside the quadrilateral. If $$\angle COD = 120$$ degrees and $$\angle BAC = 30$$ degrees, then the value of $$\angle BCD$$ (in degrees) is


Correct Answer: 90

Solution

$$\angle COD = 120$$ => $$\angle CAD = 120/2 = 60$$ (The angle subtended by the chord DC at the major arc is half the angle subtended at the centre of the circle.)
$$\angle BAC = 30$$
$$\angle BAD = \angle BAC + \angle CAD$$ = 30 + 60 = 90.
$$\angle BCD = 180 - \angle BAD$$ = 180 - 90 = 90


View Video Solution

video

Create a FREE account and get:

  • All Quant CAT Formulas and shortcuts PDF
  • 30+ CAT previous papers with solutions PDF
  • Top 500 CAT Solved Questions for Free

Comments
RAMA KRISHNA

1 month, 2 weeks ago

Since BOD is straight line, Angle BOC = 180-120=60 Degrees. Further, BOC is equilateral triangle. Hence, BCA = 60 Degrees

Free CAT Quant Questions

CAT Linear Equations

CAT Inequalities

CAT Quadratic Equations

CAT Averages, Ratios & Proportions

CAT Profit & Loss

CAT Number Systems

CAT Time, Distance & Work

CAT Geometry

CAT Progressions & Series

CAT Probability Combinatorics

CAT Venn Diagrams

CAT Data Sufficiency

CAT Logarithms, Surds & Indices

CAT Functions, Graphs & Statistics

CAT Miscellaneous

CAT DILR Questions | LRDI Questions For CAT

CAT DI Basics

CAT DI Charts

CAT Data Interpretation

CAT DI Data Change Over Period

CAT Tables With Missing Values

CAT DI Venn Diagrams

CAT DI Special Charts

CAT DI Maxima & Minima

CAT Quant-Based DI

CAT DI Connected Sets

CAT DI Miscellaneous

CAT LR Arrangement

CAT LR Selections With Conditions

CAT LR Coins & Weights

CAT LR Truth & Lie

CAT LR Puzzles

CAT LR Scheduling

CAT LR Games & Tournaments

CAT 2D & 3-D LR

CAT Quant-Based LR

CAT LR Miscellaneous

CAT Verbal Ability Questions | VARC Questions For CAT

cracku

Boost your Prep!

Download App