Three horses are grazing within a semi-circular field. In the diagram given below, AB is the diameter of the semi-circular field with center at O. Horses are tied up at P, R and S such that PO and RO are the radii of semi-circles with centers at P and R respectively, and S is the center of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi-circles and the horse tied at S can graze within the circle centred at S. The percentage of the area of the semi-circle with diameter AB that cannot be grazed by the horses is nearest to

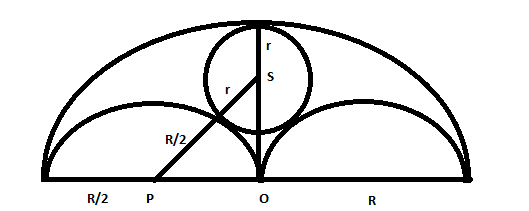
Let R be radius of big circle and r be radius of circle with centre S. Radius of 2 semicircles is R/2.
From Right angled triangle OPS, using pythagoras theorem we get
$$(r+0.5R)^2 = (0.5R)^2 + (R-r)^2$$ . We get R=3r .
Now the area of big semicircle that cannot be grazed is Area of big S.C - area of 2 semicircle - area of small circle = $$\pi*R^2$$/2 - 2*$$\pi*(0.5R)^2$$/2-$$\pi*r^2$$ = $$\pi*R^2$$/2 - 2*$$\pi*(0.5R)^2$$/2-$$\pi*(R/3)^2$$= $$\pi*R^2$$/2 - $$\pi*(R)^2$$/4-$$\pi*(R)^2$$/9 = 5*$$\pi*R^2$$/36. this is about 28 % of the area $$\pi*R^2$$/2 . Hence option B.
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free





