In a triangle ABC, AB = AC = 8 cm. A circle drawn with BC as diameter passes through A. Another circle drawn with center at A passes through Band C. Then the area, in sq. cm, of the overlapping region between the two circles is

BC is the diameter of circle C2 so we can say that $$\angle BAC=90^{\circ\ }$$ as angle in the semi circle is $$90^{\circ\ }$$
Therefore overlapping area = $$\frac{1}{2}$$(Area of circle C2) + Area of the minor sector made be BC in C1
AB= AC = 8 cm and as $$\angle BAC=90^{\circ\ }$$, so we can conclude that BC= $$8\sqrt{2}$$ cm
Radius of C2 = Half of length of BC = $$4\sqrt{2}$$ cm
Area of C2 = $$\pi\left(4\sqrt{2}\right)^2=32\pi$$ $$cm^2$$
A is the centre of C1 and C1 passes through B, so AB is the radius of C1 and is equal to 8 cm
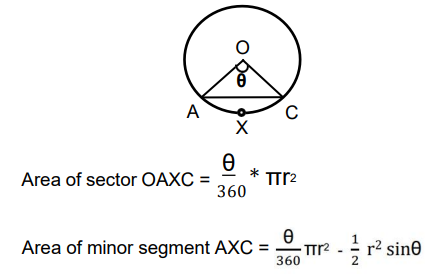
Area of the minor sector made be BC in C1 = $$\frac{1}{4}$$(Area of circle C1) - Area of triangle ABC = $$\frac{1}{4}\pi\left(8\right)^2-\left(\frac{1}{2}\times8\times8\right)=16\pi-32$$ $$cm^2$$
Therefore,
Overlapping area between the two circles= $$\frac{1}{2}$$(Area of circle C2) + Area of the minor sector made be BC in C1
= $$\frac{1}{2}\left(32\pi\right)\ +\left(16\pi-32\right)=32\left(\pi-1\right)$$ $$cm^2$$
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free