Question 56

A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is

Name: A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
Uploaded: May 3, 2022, 4:52 p.m.
Duration: 3 min 37 s
Description: A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is

Solution

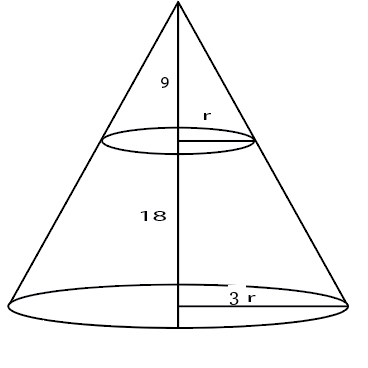
Let the base radius be 3r.

Height of upper cone is 9 so, by symmetry radius of upper cone will be r.

Volume of frustum=$$\frac{\pi}{3}\left(9r^2\cdot27-r^2.9\right)$$

Volume of upper cone = $$\frac{\pi}{3}.r^2.9$$

Difference= $$\frac{\pi}{3}\cdot9\cdot r^2\cdot25=225$$ => $$\frac{\pi}{3}\cdot r^2=1$$

Volume of larger cone = $$\frac{\pi}{3}\cdot9r^2\cdot27=243$$

Video Solution

Click on the Email ☝️ to Watch the Video Solution

Create a FREE account and get:

All Quant CAT complete Formulas and shortcuts PDF
35+ CAT previous papers with video solutions PDF
5000+ Topic-wise Previous year CAT Solved Questions for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Quadratic Equations Questions CAT Inequalities Questions CAT Averages Questions CAT Linear Equations Questions CAT Percentages Questions

CAT DILR Questions | LRDI Questions For CAT

CAT Quant Based DI Questions CAT Table with Missing values Questions CAT Selection With Condition Questions CAT Charts Questions CAT Routes And Networks Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Reading Comprehension Questions CAT Verbal Ability Questions CAT Critical Reasoning Questions CAT Odd One Out Questions CAT Vocabulary Questions

CAT 2020 QA Slot 1 Question

A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is

Video Solution

CAT Quant Questions | CAT Quantitative Ability

CAT DILR Questions | LRDI Questions For CAT

CAT Verbal Ability Questions | VARC Questions For CAT

Free Quant Questions

Login to your Cracku account

Hello! 👋

Ready to Unlock Your Success?

Please Enter Your OTP

Please enter the following details

Create a free Cracku account