Sign in
Please select an account to continue using cracku.in
↓ →
Two boys are playing on a ground. Both the boys are less than 10 years old. Age of the younger boy is equal to the cube root of the product of the age of the two boys. If we place the digit representing the age of the younger boy to the left of the digit representing the age of the elder boy, we get the age of father of the younger boy. Similarly, if we place the digit representing the age of the elder boy to the left of the digit representing the age of the younger boy and divide the figure by 2, we get the age of mother of the younger boy. The mother of the younger boy is younger to his father by 3 years. Then, what is the age of the younger boy?
Let x and y be the age of older and younger boy respectively(both single digit). According to given condition we know that $$y^2 = x$$.
Also Father's age = 10y + x and Mother's age = (10x+y)/2.
Only value which satisfies above equations is x=4 and y=2 .
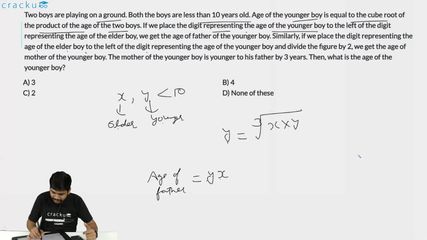
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation