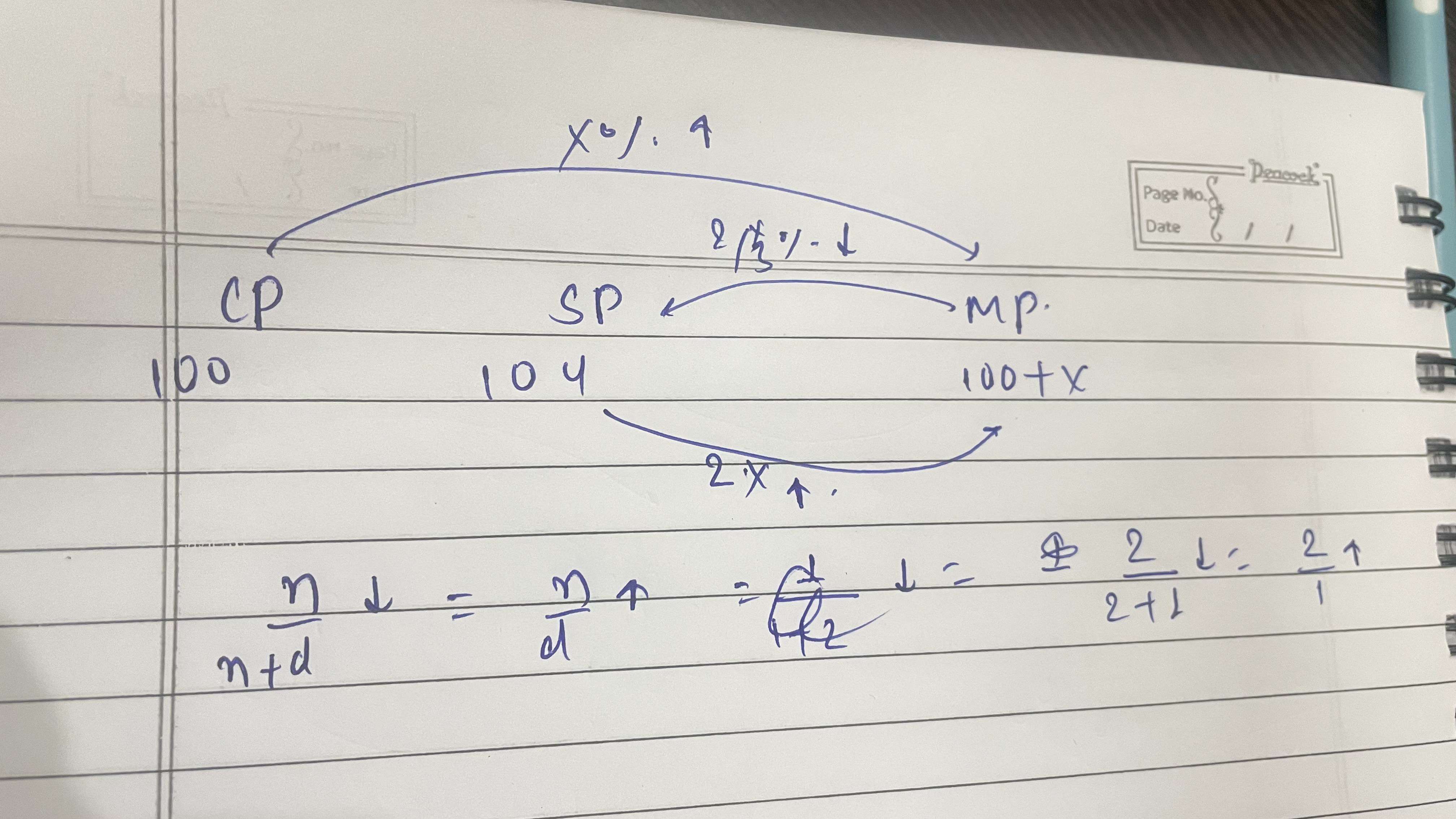
An article is marked x% above the cost price. A discount of $$\frac{2}{3}$$x% is given on the marked price. If the profit is 4% of the cost price and the value of x lies between 25 and 50, then the value of 50% of x is?
Let CP of object be a.
It is given that SP = $$(1+\frac{4}{100} )$$ x CP
$$ \Rightarrow $$ SP = 1.04 x CP
It is given that MP = $$(1+\frac{x}{100} )$$ x CP
It is also given that SP = $$(1-\frac{\frac {2x}{3}}{100} )$$ x MP
$$ \Rightarrow $$ SP = $$(1-\frac{2x}{300} )$$ x $$(1+\frac{x}{100} )$$ x CP
$$ \Rightarrow (1+\frac{4}{100})$$ x CP = $$(1-\frac{2x}{300} )$$ x $$(1+\frac{x}{100} )$$ x CP
$$ \Rightarrow (1+\frac{4}{100})$$ = $$(1-\frac{2x}{300} )$$ x $$(1+\frac{x}{100} )$$
$$ \Rightarrow \frac{104}{100}$$ = $$(1-\frac{2x}{300} )$$ x $$(1+\frac{x}{100} )$$
$$ \Rightarrow \frac{104}{100}$$ = $$(\frac{300-2x}{300} )$$ x $$(\frac{x+100}{100} )$$
$$ \Rightarrow \frac{104}{100} \times 300 \times 100$$ = $$(300-2x)$$ x $$(x+100)$$
$$ \Rightarrow 31200 $$ = $$(300-2x)$$ x $$(x+100)$$
Now, we look at the options.
Since the question says that $$x\epsilon[25,30]$$ so 50% of x ie 0.5x cannot be less than 12.50 ie $$\frac {25}{2}$$ and cannot be more than 25 ie $$\frac {50}{2}$$
This eliminates option A.
Putting values of $$x$$ given in the remaining options in the final expression, [here we need to be careful to use the value of x and not the value of 50% of x as given in the expression]
Look carefully in the remaining options : 16,13,15 as 0.5x ie 32,26,30 as possible values of x.
In the question since the discount rate offered is $$\frac{2x}{3}$$%, then a safer choice would be to check for the option of 30 in the beginning. It is a safer choice because the percentage of discount that we get in the other options are not whole numbers.
NOTE : THIS IS JUST A SAFE CHOICE AND NEVER MARK AN ANSWER DIRECTLY ON THIS PRESUMPTION WITHOUT CHECKING IT.
Putting x=30 in the expression :
(300 - (2x30))x(30+100) = (300-60)x(100+30) = 240x130 = 24x13x100= 312x100 = 31200= LHS of expression.
Thus the value of $$x$$ is 30.
Therefore value of 50% of $$x$$ = 0.5x30 = 15
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE