Please enter the following details
Comprehension:
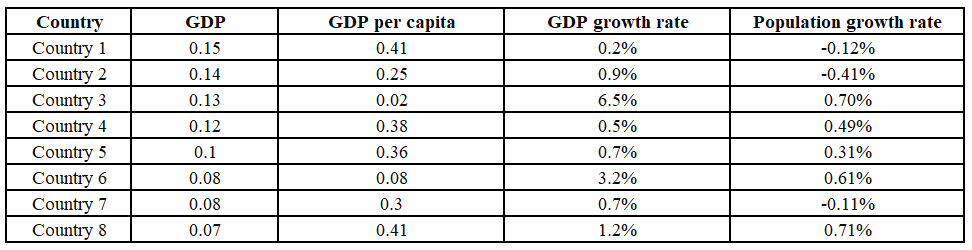
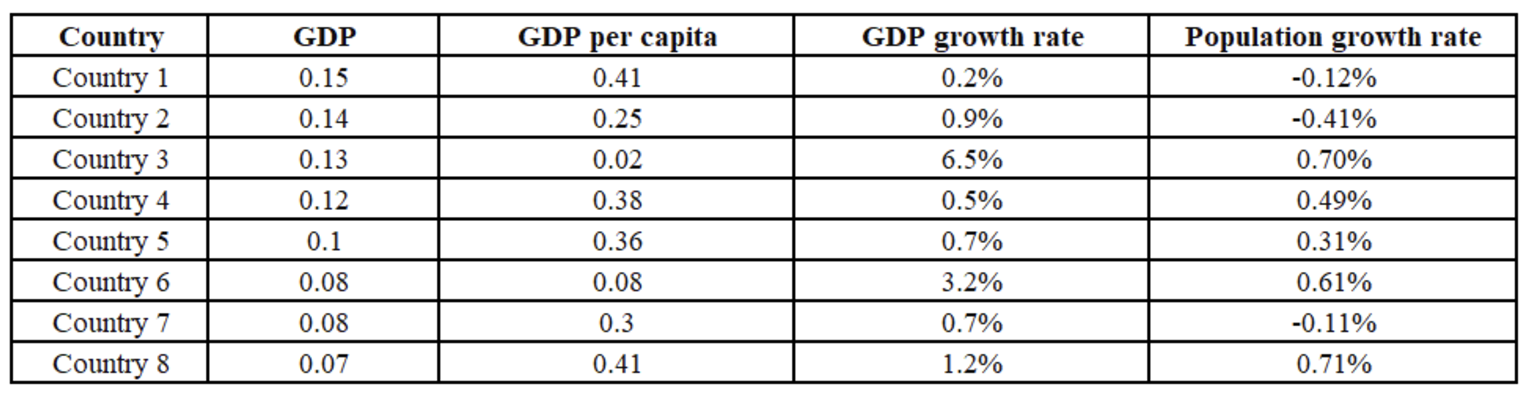
Out of 10 countries -- Country 1 through Country 10 -- Country 9 has the highest gross domestic product (GDP), and Country 10 has the highest GDP per capita. GDP per capita is the GDP of a country divided by its population. The table below provides the following data about Country 1 through Country 8 for the year 2024.
• Column 1 gives the country's identity.
• Column 2 gives the country’s GDP as a fraction of the GDP of Country 9.
• Column 3 gives the country’s GDP per capita as a fraction of the GDP per capita of Country10.
• Column 4 gives the country’s annual GDP growth rate.
• Column 5 gives the country’s annual population growth rate.
Assume that the GDP growth rates and population growth rates of the countries will remain constant for the next three years.
Which one among the countries 1, 4, 5, and 7 will have the largest population in 2027?
We are given the following table,
This table compares the GDP, GDP per capita, and population of eight countries, all of which are referenced using a consistent set of units.
Specifically, the GDP values are all given with the same country as the reference point (The reference point being Country 9)
Similarly, the GDP per capita among the eight countries in the table is given using the same reference point (The reference point being Country 10)
As a result, when comparing two countries from the list in terms of GDP, GDP per capita, or population, we can directly use the values presented in the table, since they are all based on a uniform reference point.
We can compare the population of two countries using the formula, $$Population=\dfrac{GDP}{GDP\ Per\ Capita}$$
For example, to compare the GDP of Country A and Country B, we can simply use the values listed under "GDP" in the table, as both are referenced using the same country throughout. This eliminates the need for additional conversions or adjustments.
The given question asks us to compare the population of countries between 1, 4, 5, and 7 in the year 2027
Country 1: Population in 2024 will be 0.15/0.41 or 15/41 and the population is decreasing at the rate 0.12%
Country 4: Population in 2024 will be 0.12/0.38 or 12/38 and the population is increasing at the rate of 0.49%
Country 5: Population in 2024 will be 0.1/0.36 or 10/36 and the population is increasing at the rate 0.31%
Country 7: Population in 2024 will be 0.08/0.3 or 8/30 and the population is decreasing at the rate 0.11%
Simplifying and comparing the four fractions in order, $$\frac{15}{41}$$, $$\frac{6}{19}$$, $$\frac{5}{18}$$, $$\frac{4}{15}$$
The decimal values of the following are: 0.36586, 0.315789, 0.2777, 0.2666
Right away we can eliminate Country 7 since the population is not only the least, but it is decreasing, so there is no chance it will have the highest population in three years time.
For the other three countries,
Country 1: $$\left(0.36585\right)\times\ \left(0.9988\right)^3$$ this equals 0.36453
Country 4: $$\left(0.315789\right)\times\ \left(1.0049\right)^3$$ this equals 0.32045
Country 7: $$\left(0.2777\right)\times\ \left(1.0031\right)^3$$ this equals 0.2803612
Hence, Country 1 will have the largest population among these four countries.
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
