A one rupee coin is placed on a table. The maximum number of similar one rupee coins which can be placed on the table, around it, with each one of them touching it and only two others is
Considering the centre coin which is denoted by C1.
The surrounding coins are of equal radius as the centre coin. Since each coin is placed next to each other and considering the total number of coins = n.
The pairs formed by the coins which touch the consecutive coins is given by :
(1, 2) , (2, 3) ........... (n, 1)
The triangles formed by joining the centres of all the consecutive circles at the centre of C1 = 360 degrees.
If we join centres of 2 outer circles with the centre circle, it will make an equilateral triangle.
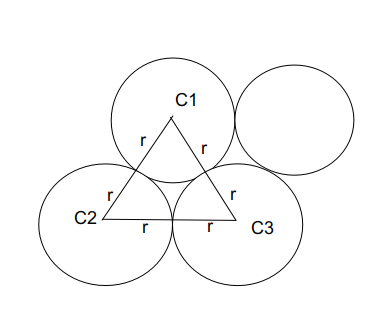
A single pair forms 60 degrees as it forms an equilateral triangle. Hence $$\frac{360}{n}=\ 60$$
n = 6
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free




