CAT WhatsApp Group
Sign in
Please select an account to continue using cracku.in
↓ →
CAT WhatsApp Group
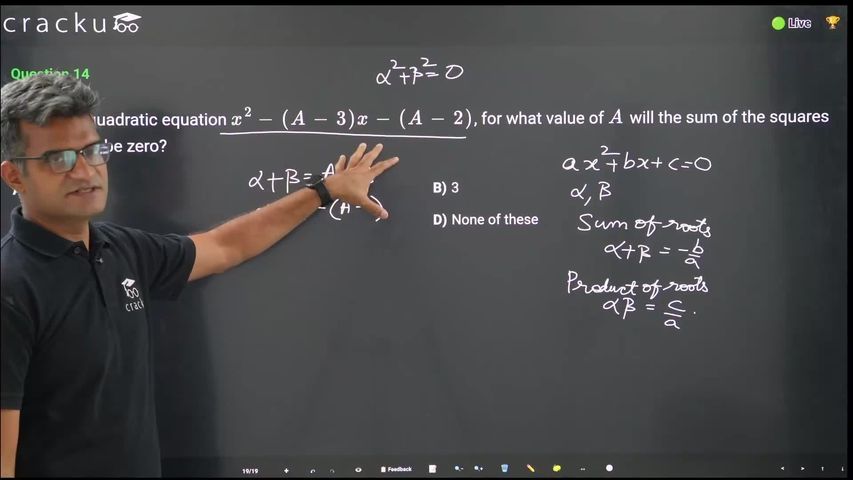
Given the quadratic equation $$x^2 - (A - 3)x - (A - 2)$$, for what value of $$A$$ will the sum of the squares of the roots be zero?
For summation of square of roots to be zero, individual roots should be zero.
Hence summation should be zero i.e. A-3=0 ; A = 3
And product of roots will also be zero i.e. A-2 = 0 ; A =2
So there is no unique value of A which can satisfy above equation.
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation
Ask our AI anything
AI can make mistakes. Please verify important information.
AI can make mistakes. Please verify important information.
