Sign in
Please select an account to continue using cracku.in
↓ →
CAT WhatsApp Group
The figure shows the rectangle ABCD with a semicircle and a circle inscribed inside in it as shown. What is the ratio of the area of the circle to that of the semicircle?
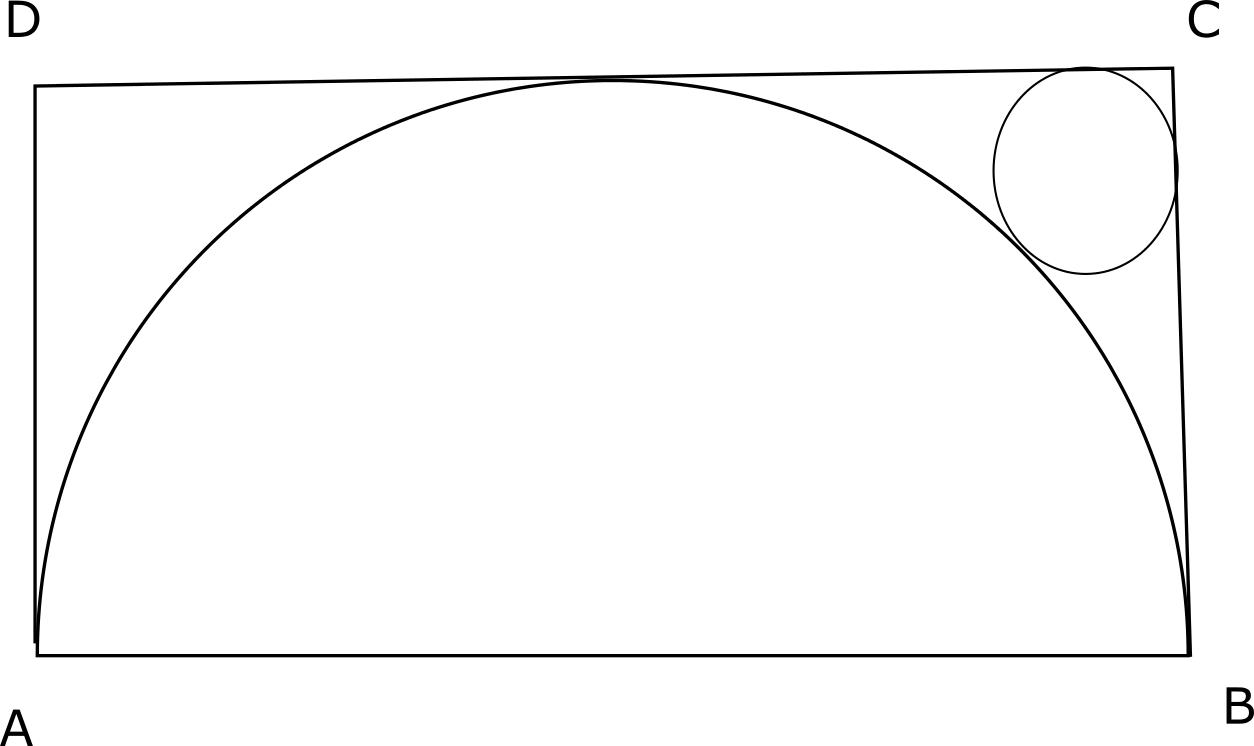
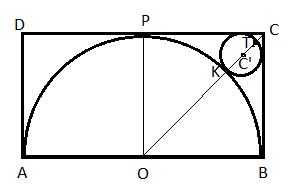
Let the center be O and the point at which the semicircle intersects CD be P.
Let the radius of the semicircle be R and the circle be r.
OP = R and OC = R$$\sqrt{2}$$
OC - OT = CC' - TC'
$$R\sqrt{2} - R - 2r$$ = $$r\sqrt{2} - r$$
=> $$R\sqrt{2} - R$$ = $$r\sqrt{2} + r$$
=> r = $$\frac{(\sqrt{2}-1)R}{\sqrt{2}+1}$$
=> r = $$(\sqrt{2}-1)^2$$R
Ratio of areas will be $$r^2 : \frac{R^2}{2}$$ = $$2(\sqrt{2}-1)^4$$ : 1
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Book Free CAT Mentorship
Get personalized CAT strategy from a 99%iler
500+ students mentored
OTP Verification
Enter the 6-digit code sent to your phone
Booking Summary
Enter OTP
Didn't receive the OTP?
Start your IIM journey with the right preparation and crack CAT 2026.
Educational materials for CAT preparation
Ask our AI anything
AI can make mistakes. Please verify important information.
AI can make mistakes. Please verify important information.
91- 6303239042
