Sixteen patients in a hospital must undergo a blood test for a disease. It is known that exactly one of them has the disease. The hospital has only eight testing kits and has decided to pool blood samples of patients into eight vials for the tests. The patients are numbered 1 through 16, and the vials are labelled A, B, C, D, E, F, G, and H. The following table shows the vials into which each patient’s blood sample is distributed.
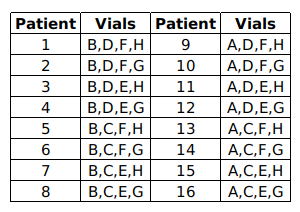
If a patient has the disease, then each vial containing his/her blood sample will test positive. If a vial tests positive, one of the patients whose blood samples were mixed in the vial has the disease. If a vial tests negative, then none of the patients whose blood samples were mixed in the vial has the disease.
Suppose vial C tests positive and vials A, E and H test negative. Which patient has the disease?
The patients in
Vial A: 9, 10, 11, 12, 13, 14, 15, 16
Vial B: 1, 2, 3, 4, 5, 6, 7, 8.
Vial C: 5,6,7,8,13,14,15,16
Vial D:1,2,3,4,9,10,11,12
Vial E:3,4,7,8,11,12,15,16
Vial F:1,2,5,6,9,10,13,14
Vial G:2,4,6,8,10,12,14,16
Vial H:1,3,5,7,9,11,13,15
If vial C tests positive and vials A, E and H test negative then Patient 6 must have disease as all other patients in Vial C expect patient 6 are present in at least one of A, E, H.
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
