If r is a constant such that $$\mid x^2 - 4x - 13 \mid = r$$ has exactly three distinct real roots, then the value of r is

The quadratic equation of the form $$\mid x^2 - 4x - 13 \mid = r$$ has its minimum value at x = -b/2a, and hence does not vary irrespective of the value of x.

Hence at x = 2 the quadratic equation has its minimum.

Considering the quadratic part : $$\left|x^2-4\cdot x-13\right|$$. as per the given condition, this must-have 3 real roots.

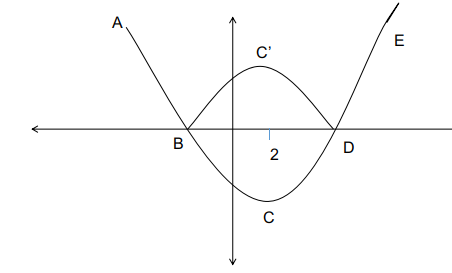
The curve ABCDE represents the function $$\left|x^2-4\cdot x-13\right|$$. Because of the modulus function, the representation of the quadratic equation becomes :

ABC'DE. 

There must exist a value, r such that there must exactly be 3 roots for the function. If r = 0 there will only be 2 roots, similarly for other values there will either be 2 or 4 roots unless at the point C'.

The point C' is a reflection of C about the x-axis. r is the y coordinate of the point C' :

The point C which is the value of the function at x = 2, = $$2^2-8-13$$

= -17, the reflection about the x-axis is 17.

Alternatively,

$$\mid x^2 - 4x - 13 \mid = r$$ .

This can represented in two parts :

$$x^2-4x-13\ =\ r\ if\ r\ is\ positive.$$

$$x^2-4x-13\ =\ -r\ if\ r\ is\ negative.$$

Considering the first case : $$x^2-4x-13\ =r$$

The quadraticequation becomes : $$x^2-4x-13-r\ =\ 0$$

The discriminant for this function is : $$b^2-4ac\ =\ 16-\ \left(4\cdot\left(-13-r\right)\right)=68+4r$$

SInce r is positive the discriminant is always greater than 0 this must have two distinct roots.

For the second case :

$$x^2-4x-13+r\ =\ 0$$ the function inside the modulus is negaitve

The discriminant is $$16\ -\ \left(4\cdot\left(r-13\right)\right)\ =\ 68-4r$$

In order to have a total of 3 roots, the discriminant must be equal to zero for this quadratic equation to have a total of 3 roots.

Hence $$\ 68-4r\ =\ 0$$

r = 17, for r = 17 we can have exactly 3 roots.