XAT 2010 Question Paper
Answer questions based on the following information:
An automobiles company’s annual sales of its small cars depends on the state of the economy as well as on whether the company uses some high profile individual as its brand ambassador in advertisements of its product. The state of the economy is “good”, “okay” and “bad” with probabilities 0.3, 0.4 and 0.3 respectively. The company may choose a high profile individual as its brand ambassador in TV ads or may go for the TV ads without a high profile brand ambassador.
If the company fixes price at Rs. 3.5 lakh, the annual sales of its small cars for different states of the economy and for different kinds of TV ads are summarized in table 1. The figures in the first row are annual sales of the small cars when the company uses a high profile individual as its brand ambassador in its TV ads and the ones in the second row are that when the company does not use any brand ambassador in TV ads, for different states of the economy.
Table 1:

Without knowing what exactly will be the state of the company in the coming one year, the company will either have to sign a TV ad contract with some high profile individual, who will be the company’s brand ambassador for its small car for the next one year, or go for a TV ad without featuring any high profile individual. It incurs a cost of Rs. 3.45 lakh (excluding the payment to the brand ambassador) to put a car on the road.
When the company’s profit is uncertain, the company makes decisions on basis of its expected profit. If the company can earn a profit xi with probability pi (the probability depends on the state of economy), then the expected profit of the company is $$\sum_1XiPi$$
XAT 2010 - Question 71
Mr. Khan a popular film actor, agrees to sign the contract to become the company’s brand ambassador for Rs. 9 crore. The cost to the company of putting a car on the road also got escalated by Rs. 1000. If the company signs the contract with Mr.Khan, its profit will
For the following questions answer them individually
XAT 2010 - Question 72
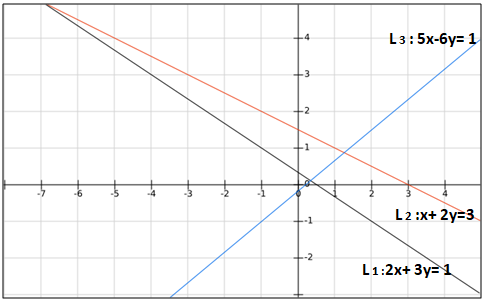
Determine the value(s) of “a” for which the point $$(a, a^{2})$$ lies inside the triangle formed by the lines: 2x+ 3y= 1, x+ 2y=3 and 5x-6y= 1
XAT 2010 - Question 73
The supervisor of a packaging unit of a milk plant is being pressurised to finish the job closer to the distribution time, thus giving the production staff more leeway to cater to last minute demand. He has the option of running the unit at normal speed or at 110% of normal - “fast speed”. He estimates that he will be able to run at the higher speed for 60% of the time. The packet is twice as likely to be damaged at the higher speed which would mean temporarily stopping the process. If a packet on a randomly selected packaging runs has probability of 0.112 of damage, what is the probability that the packet will not be damaged at normal speed?
Let $$A_{1},A_{2},.....A_{n}$$ be then points on the straight - line y = px + q. The coordinates of $$A_{k}is(X_{k},Y_{k})$$, where k = 1, 2, ...n such that $$X_{1},X_{2}....X_{n}$$ are in arithmetic progression. The coordinates of $$A_{2}$$ is (2,–2) and $$A_{24}$$ is (68, 31).
XAT 2010 - Question 75
The number of point(s) satisfying the above mentioned characteristics and not in the first quadrant is/are
For the following questions answer them individually
XAT 2010 - Question 76
The operation (x) is defined by
(i) (1) = 2
(ii)(x + y) = (x).(y)
for all positive integers x and y.
If $$\sum_{x=1}^n(x)$$ = 1022 then n =
XAT 2010 - Question 77
Amarendra and Dharmendra are brothers. One day they start at the same time from their home for Tatanagar railway station in their respective cars. Amarendra took 25 minutes to reach the station. After reaching the station Amarendra found that Dharmendra is 2500 m away from the station. The distance of Tatanagar Station from their home is 15 km. Next day Dharmendra decided to start 7 minutes early.
If they drive at the speed same as the previous day then Amarendra will reach the station
XAT 2010 - Question 78
Let $$S_{1}, S_{2},...$$ be the squares such that for each n ≥ 1, the length of the diagonal of $$S_{n}$$ is equal to the length of the side of $$S_{n+1}$$. If the length of the side of $$S_{3}$$ is 4 cm, what is the length of the side of $$S_{n}$$ ?
XAT 2010 - Question 79
In a clock having a circular scale of twelve hours, when time changes from 7:45 A.M. to 7:47 A.M.,
by how many degrees the angle formed by the hour hand and minute hand changes?
Questions are followed by two statements labelled as I and II. Decide if these statements are sufficient to conclusively answer the question. Choose the appropriate answer from the options given below:
A. Statement I alone is sufficient to answer the question.
B. Statement II alone is sufficient to answer the question.
C. Statement I and Statement II together are sufficient, but neither of the two alone is sufficient to answer the question.
D. Either Statement I or Statement II alone is sufficient to answer the question.
E. Both Statement I and Statement II are insufficient to answer the question
XAT 2010 - Question 80
In the trapezoid PQRS, PS is parallel to QR. PQ and SR are extended to meet at A. What is the value of $$\angle$$PAS ?
I. PQ = 3, RS = 4 and $$\angle$$ QPS = 60°.
II. PS = 10, QR = 5.

.webp)


