SRCC GBO Sample Paper 2026

Let the price at which Ankur purchases a mobile phone and a laptop be X and Y.

Therefore, the cost price of 20 mobile phones and 10 laptops = 20X+10Y = 14,00,000   ----equation (1)

Now, it is given that he sold a mobile phone at an increased price of 30% and a laptop for an increased price of 20%

Profit made = 3,50,000

Therefore, the Selling Price of 20 mobile phones and 10 laptops = 14,00,000+3,50,000 = 17,50,000

=> 20X*1.3+10Y*1.2 = 17,50,000

=> 26X+12y = 17,50,000 ----equation (2)

Solving equations (1) and (2), we get

X =  35,000 and Y = 70,000

Therefore, if he has sold each mobile phone at a 40% increased price and each laptop at a 50% increased price.

The profit will be 20*35,000*0.4 + 10*70,000*0.5 = 2,80,000+3,50,000 = Rs.6,30,000

Compound Interest on₹5,000 for 2 years will be at a rate of R will be $$5000\left(1+\frac{R}{100}\right)^2-5000=4800$$

$$5000\left(1+\frac{R}{100}\right)^2=9800$$

$$\left(1+\frac{R}{100}\right)^2=\frac{9800}{5000}=1.96$$

$$\left(1+\frac{R}{100}\right)=1.4$$

R = 40%

Simple interest = $$\frac{PTR}{100}$$

Simple interest for ₹ 5000 at 40% for 2 years will be $$\frac{5000*40\cdot2}{100}=4000$$

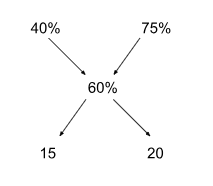
It is given that the concentration of mixture A is 40% and the concentration of mixture B is 75%. The resulting mixture C has 3L of milk in 5L of the mixture. So, the concentration of the mixture is calculated as,

Concentration of milk in C = $$\dfrac{3}{5}\ \times\ 100\ =\ 60\%$$

Using the allegation method, we can calculate the ratio in which they are mixed to be as,

So, the ratio at which they must be mixed is 15:20 = 3:4.

The correct answer is option B.

The 10th, 11th, and 12th elements in the series are the first three elements of the last 16. And the average of 16 numbers is 60. To maximize the first three of these 16, we should keep the numbers as close to 60 as possible. So, the numbers will be 52, 53, 54, 55, ..., 59,61, ...,65, 66, 67, 68.

The 10th, 11th, and 12th elements in the series are the last three elements of the first 12.  Let us check if 52, 53, and 54 will satisfy the average or not.

The sum of the first 12 will be 30*12 = 360.

The sum of the first nine will be 360 - (52+53+54) = 201.

The sum of nine distinct positives can be 201. 

So, 52, 53, and 54 will be the maximum possible values for the 10th, 11th, and 12th elements in the series. Their average will be 53.

We are given that,

$$\sqrt{\ \dfrac{7\ +\ 4\sqrt{\ 3}}{3}}\ =\ a\ +\ b\sqrt{\ 3}$$

LHS can be written as,

$$\sqrt{\ \dfrac{\left(7\ +\ 4\sqrt{\ 3}\right)\times\ 3}{3\ \times\ 3}}\ =\ \sqrt{\dfrac{21\ +\ 12\sqrt{\ 3}}{9}\ }=\ \ \sqrt{\dfrac{3^2\ +\ 2\times\ 3\times\ 2\sqrt{\ 3}\ +\ \left(2\sqrt{\ 3}\right)^2}{3^2}\ }\ =\ \sqrt{\left(\ \dfrac{3\ +\ 2\sqrt{\ 3}}{3}\right)^{^2}}\ =\ 1\ +\ \dfrac{2}{3}\sqrt{\ 3}$$

The value of a is 1, and b is $$\dfrac{2}{3}$$.

The value of $$a\ -\ b\ =\ 1\ -\ \dfrac{2}{3}\ =\ \dfrac{1}{3}$$

The correct answer is option C.

The equations given are,

$$\dfrac{3}{x}\ +\ \dfrac{4}{y\ }\ =\ 3$$

$$-\dfrac{2}{x}\ +\ \dfrac{1}{y\ }\ =\ -13$$

Let us assume the value of $$\dfrac{1}{x}$$ to be a and $$\dfrac{1}{y}$$ to be b. The above equations become,

3a + 4b = 3 ----(1)

-2a + b = -13 ----(2)

(1) * 2 + (2) * 3, we get,

(3a + 4b)*2 + (-2a + b)*3 = 3 * 2 + (-13) * 3

6a + 8b - 6a + 3b = 6 - 39

11b = -33

b = -3 and a = 5

We get the values x and y as,

$$\dfrac{1}{x}\ =\ 5$$

$$x\ =\ \dfrac{1}{5}$$

$$\dfrac{1}{y}\ =\ -3$$

$$y\ =\ -\dfrac{1}{3}$$

$$x\ +\ y\ =\ \dfrac{1}{5}-\dfrac{1}{3}\ =\ -\dfrac{2}{15}$$

$$15\left(x\ +\ y\right)\ =\ -\dfrac{2}{15}\ \times\ 15\ \ =\ -2$$

The correct answer is option C.

Given that a and b are the roots of the equation $$x^2\ -\ 13x\ +\ 42\ =\ 0$$

Sum of the roots = a + b =  $$-\dfrac{b}{a}$$  =  $$-\dfrac{\left(-13\right)}{1}$$  = 13

Product of the roots = ab = $$\dfrac{c}{a}$$ = $$\dfrac{42}{1}$$  = 42

Let the new quadratic equation be $$x^2\ +\ cx\ +\ d\ =\ 0$$. For the new equation with roots as $$\dfrac{1}{a}$$ and $$\dfrac{1}{b}$$, the sum of the roots and product of the roots can be calculated as

Sum of the roots =  $$\dfrac{1}{a}\ +\ \dfrac{1}{b}$$  =  $$\dfrac{a\ +\ b}{ab}$$ = $$\dfrac{13}{42}$$ = -c

Product of the roots =  $$\dfrac{1}{a}\times\ \dfrac{1}{b}$$  =  $$\dfrac{1}{ab}$$  =  $$\dfrac{1}{42}$$  = d

So, the new equation becomes,

$$x^2\ -\ \dfrac{13}{42}x\ +\ \dfrac{1}{42}\ =\ 0$$

Multiplying the whole equation by 42, we get,

$$42x^2\ -\ 13x\ +\ 1\ =\ 0$$

The correct answer is option A.

Given inequality is, $$\dfrac{\left(x\ -\ 3\right)^2\left(x\ ^2\ +\ 9x\ +\ 20\right)}{\left(x^2\ +\ 2x\ -\ 15\right)}\ \le\ 0$$

$$x\ ^2\ +\ 9x\ +\ 20\ $$ can be written as,

$$x\ ^2\ +\ 4x\ \ +\ 5x\ +\ 20\ $$  =  $$x\ \left(x\ +\ 4\right)\ \ +\ 5\left(x\ +\ 4\right)\ $$  =  $$\left(x\ +\ 5\right)\left(x\ +\ 4\right)\ $$

$$x\ ^2\ +\ 2x\ -\ 15\ $$ can be written as,

$$x\ ^2\ -\ 3x\ \ +\ 5x\ -\ 15\ $$ = $$x\ \left(x\ -\ 3\right)\ \ +\ 5\left(x\ -\ 3\right)\ $$ = $$\left(x\ +\ 5\right)\left(x\ -\ 3\right)\ $$

The inequality can be written as,

$$\dfrac{\left(x\ -\ 3\right)^2\left(x\ +\ 4\right)\left(x\ +\ 5\right)}{\left(x-\ 3\right)\left(x\ +\ 5\right)}\ \le\ 0$$

We can cancel the terms (x - 3) and (x + 5) from the numerator and denominator with the condition that x cannot take the values 3 and - 5.

After cancellation, the equation becomes,

$$\left(x\ -\ 3\right)\left(x\ +\ 4\right)\ \le\ 0$$

So, the values x can take are [-4, 3). We cannot include 3 as we already obtained the condition above.

So, the correct answer is option C.

Given that,

$$f\left(x\right)\ =\ 2x^2\ +\ 3x\ +\ 1$$

$$g\left(x\right)\ =\ 3x\ +\ 1$$

The value of $$f\left(g\left(x\right)\right)$$ is given as,

$$f\left(g\left(x\right)\right)\ =\ 2\left(3x\ +\ 1\right)^2\ +\ 3\left(3x\ +\ 1\right)\ +\ 1\ =\ 2\left(9x^2\ +\ 6x\ +\ 1\right)\ +\ 9x\ +\ 4\ =\ 18x^2\ +\ 21x\ +\ 6$$

$$g\left(f\left(x\right)\right)\ =\ 3\left(2x^2\ +\ 3x\ +\ 1\right)\ +\ 1\ =\ 6x^2\ +\ 9x\ +\ 4$$

Equating f(g(x)) and g(f(x)), we get,

$$18x^2\ +\ 21x\ +\ 6\ =\ 6x^2\ +\ 9x\ +\ 4$$

$$12x^2\ +\ 12x\ +\ 2\ =\ 0$$

We can see that D > 0 for the above equation, and the roots of the equation are real. So, the sum of all the possible values of x is given by,

Sum of the roots  = $$-\dfrac{b}{a}$$ = $$-\dfrac{12}{12}$$ = $$-1$$

The correct answer is option D.

We are given the equation,

$$f\left(x\right)\ +\ 2f\left(\dfrac{1}{1-x}\right)\ =\ x$$

Substituting the value of x = 2 in the equation, we get,

$$f\left(2\right)\ +\ 2f\left(-1\right)\ =\ 2$$   -----(1)

Substituting x = -1, we get

$$f\left(-1\right)\ +\ 2f\left(\dfrac{1}{2}\right)\ = -1$$   -----(2)

Substituting x = $$\dfrac{1}{2}$$ we get,

$$f\left(\dfrac{1}{2}\right)\ +\ 2f\left(2\right)\ =\ \dfrac{1}{2}$$   -----(3)

By applying  (1) - 2*(2) + 4*(3), we get,

$$f\left(2\right)\ +\ 2f\left(-1\right)\ -\ 2f\left(-1\right)\ -\ 4f\left(\dfrac{1}{2}\right)\ +\ 4f\left(\dfrac{1}{2}\right)\ +\ 8f\left(2\right)\ =\ 2\ -\ 2\times\ \left(-1\right)\ +\ \ 4\times\ \dfrac{1}{2}$$

$$f\left(2\right)+\ 8f\left(2\right)\ =\ 2\ +\ 2\ +\ 2$$

$$9f\left(2\right)\ =\ 6$$

$$f\left(2\right)\ =\ \dfrac{2}{3}$$

The correct answer is option A.