CUET PG 2023 Question Paper COQP12 Shift-2
For the following questions answer them individually
The heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4. Find the ratio of their volumes?
If the surface areas of two spheres are in the ratio of 4 : 25, then the ratio of their volumes is:
If $$a^{2} + b^{2} + \frac{1}{a^{2}} + \frac{1}{b^{2}} = 4$$ then the value of $$a^{2} + b^{2}$$
$$a + b + c = 6, a^{2} + b^{2} + c^{2} = 14$$ and $$a^{3} + b^{3} + 3 = 36$$, then the value of abc is:
Below question contains two equations as I and II. You have to solve both equations and determine the relationship between them and choose correct option:
I. $$2x^{2} + 3x - 35 = 0$$
II. $$4y^{2} + 10y - 104 = 0$$
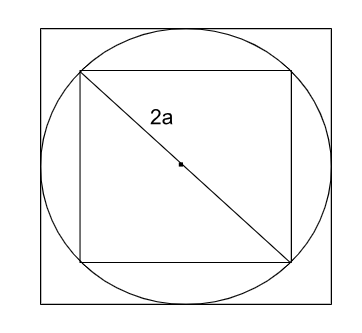
A square is inscribed in a circle of diameter 2a and another square is circumscribing circle. The difference between the areas of outer and inner squares is:
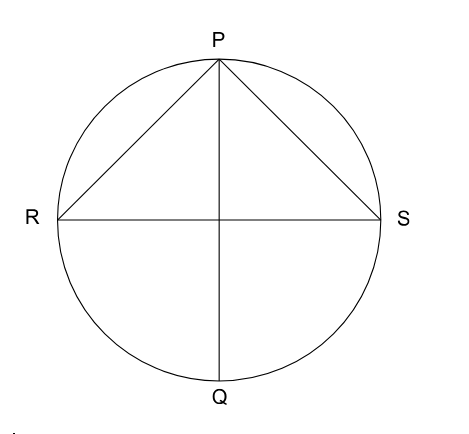
If PQ and RS are two diameters of a circle of radius rand they are mutually perpendicular, then what is the ratio of the area of the circle to the area of the $$\triangle PRS$$?
Find the value of $$\frac{1}{4 \times 5} + \frac{1}{5 \times 6} + \frac{1}{6 \times 7} + ....... + \frac{1}{10 \times 11}$$:
If $$x$$ is an integer such that $$x +\frac{1}{x} = \frac{17}{4}$$, then the value of $$x - \frac{1}{x}$$:
