If PQ and RS are two diameters of a circle of radius rand they are mutually perpendicular, then what is the ratio of the area of the circle to the area of the $$\triangle PRS$$?

If PQ and RS are two diameters of a circle of radius r, then they are mutually perpendicular.

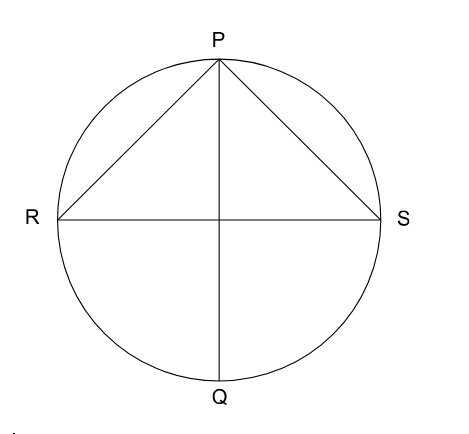
RS = 2r (Where r is the radius of the circle)

RP = RS = $$r\sqrt{2}$$

Area of circle = $$\pi r^2$$

Triangle SPR is a right-angled triangle, right-angled at P.  (Angle RPS is 90 degrees as RS is the diameter)

Area of $$\triangle PRS$$ = $$\dfrac{1}{2}\times PR\times\ PS$$ = $$\dfrac{1}{2}\times r\sqrt{2}\times\ r\sqrt{2}$$ = $$r^2$$

Thus, the ratio is $$\pi r^2$$:$$r^2$$ = $$\pi:1$$