Geometry

Consider parallel lines AB, CD and EF as shown in the figure.

• XY and MN are known as transversals

• $$\angle $$ XPQ = $$\angle $$ PRS = $$\angle $$ RTU as corresponding angles are equal

• Interior angles on the side of the transversal are supplementary. i.e. $$\angle $$ PQS + $$\angle $$ QSR = 180 degrees

• Exterior angles on the same side of the transversal are supplementary. i.e. $$\angle $$ MQB + $$\angle $$ DSU = 180 degrees.

• Two transversals are cut by three parallel lines in the same ratio i.e. PR / RT = QS / SU

Triangles

• The Sum of all angles in a triangle is 180 degrees

• An angle less than 90 degrees is called an acute angle. An angle greater than 90 degrees is called an Obtuse angle.

• A triangle with all sides unequal is called a Scalene triangle.

  Nomenclature

• A line joining the midpoint of a side with the opposite vertex is called a Median.

• A perpendicular drawn from a vertex to the opposite side is called the Altitude.

• The three perpendicular bisectors of a triangle meet at a point called the Circumcentre. A circle drawn from this point with the circumradius would pass through all the vertices of the triangle.
• The three angle bisectors of a triangle meet at a point called the incentre of a triangle. The incentre is equidistant from the three sides and a circle drawn from this point with the inradius would touch all the sides of the triangle.
• The point of intersection of the three altitudes is the Orthocentre.

• The point of intersection of the three medians is the Centroid.

• A triangle with two sides equal is called an Isosceles triangle. The two angles of an isosceles triangle that are not contained between the equal sides are equal.
  

• A triangle with all sides equal is called an equilateral triangle. All angles of an equilateral triangle equal 60 degrees.

• The Sum of any two sides of a triangle is always greater than the third side.
• The difference between any two sides of a triangle is always lesser than its third side.
• If in a triangle all of its angles are less than 90^{0} then that triangle is called an Acute-angled triangle.
• A triangle with one of its angles equal to 90^{0} then that triangle is called a Right-angled triangle.
• A triangle with one of its angles greater than 90^{0} then that triangle is called an Obtuse angled triangle.
• If one side of a triangle is produced then that exterior angle formed is equal to the sum of opposite remote interior angles.
• A line that bisects and also makes a right angle with the same side of the triangle is called a Perpendicular bisector.
  A line that divides the angle at one of the vertices into two parts is called an Angular bisector.
• Pythagoras theorem: In a right angled triangle ABC where $$\angle $$B=90 degrees, $$ AC^2$$ = $$AB^2$$ + $$BC^2$$
• Apollonius theorem states that in a triangle ABC if AD is a median to BC then $$AB^2+AC^2=2\cdot\left(AD^2+BD^2\right)$$

If x is the side of an equilateral triangle, then the

Altitude (h) =$$\frac{\sqrt{\ 3}}{2}x$$

Area =$$\frac{\sqrt{\ 3}}{4}x^2$$

Inradius = $$\frac{1}{3}\times\ h$$

Circumradius = $$\frac{2}{3}\times\ h$$

▪ Area of an isosceles triangle =$$\frac{a}{4}\sqrt{\ 4c^2-a^2}$$ (where a, b and c are the length of the sides of BC, AC and AB respectively b = c)

If a, b, and c are the lengths of the right-angled triangles, with 'c' being the hypotenuse, then

Circumradius = $$\dfrac{h}{2}$$

Inradius = $$\dfrac{\left(a+b-c\right)}{2}$$

Special triangles :

30, 60 and 90 degrees

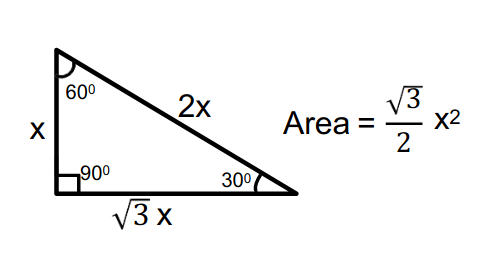
45, 45 and 90 degrees

Area of a triangle A

• $$A$$ = $$\sqrt{s(s-a)(s-b)(s-c)}$$ where s =$$\frac{\left(a+b+c\right)}{2}$$.
• A =$$\frac{1}{2}\times\ base\times\ altitude$$
• 
• Application:
• In the above triangle, both the triangles ADB and ADC have the same height => The ratio of the areas of triangles ADB and ADC will be in the ratio of their bases BD and DC $$\dfrac{Area\left(ADB\right)}{Area\left(ADC\right)}=\dfrac{BD}{DC}$$
• A = $$\frac{1}{2}\times\ a\times\ b\times\ \sin C$$, where C is the enclosed angle between sides a and b.
• A = $$\frac{abc}{4R}$$ where R is the circumradius
• So, for a right-angled triangle with a,b, and c as the sides, with c as the hypotenuse [Angle C = 90 degrees]
• A = $$\dfrac{1}{2}\times\ a\times\ b\times\ \sin\left(90\right)=\dfrac{abc}{4R}$$ => $$R=\dfrac{c}{2}$$
• A = rs where r is the inradius and s is the semi-perimeter.
• The area of a triangle with inradius r and circumradius R is r(r+2R)

Mid-Point Theorem: The line joining the midpoint of any two sides in a triangle is parallel to the third side and is half the length of the third side. If X is the midpoint of CA and Y is the midpoint of CB, then XY will be parallel to AB and XY = ½ * AB

Basic proportionality theorem: If a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the ratio of respective sides. If in a triangle ABC, D and E are the points lying on AB and BC respectively and DE is parallel to AC then AD/DB = EC/BE

Interior Angular Bisector theorem: In a triangle, the angular bisector of an angle divides the side opposite to the angle, in the ratio of the remaining two sides. In a triangle ABC if AD is the angle bisector of angle A then AD divides the side BC in the same ratio as the other two sides of the triangle. i.e. BD/ CD= AB/AC.

Exterior Angular Bisector theorem: The angular bisector of the exterior angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. In a triangle ABC, if CE is the angular bisector of exterior
angle BCD of a triangle, then AE/BE = AC/BC

Similarity and Congruence:

Similar triangles :
If two triangles are similar then their corresponding angles are equal and the corresponding sides will be in proportion.
For any two similar triangles :

▪ Ratio of sides = Ratio of medians = Ratio of heights = Ratio of circumradii = Ratio of Angular bisectors.
▪ Ratio of areas = Ratio of the square of the sides.

Tests of similarity : (AA / SSS / SAS)

Congruent triangles

If two triangles are congruent then their corresponding angles and their corresponding sides are equal.

Tests of congruence : (SSS / SAS / AAS / ASA)

Circle Formulae
1. Area: $$\pi\ r^2$$
2. Circumference: $$2\pi r$$
3. Length of Arc: $$\left(\frac{\theta}{360}\right)\left(2\pi r\right)$$
4. Area of Sector: $$\left(\frac{\theta}{360}\right)\left(\pi r^2\right)$$

1. The perpendicular drawn from the center of a circle to a chord bisects the chord, Conversely, the line joining the mid-point of a chord and the center of the circle, is perpendicular to the chord.
2. Chords that are equal are equidistant from the center of the circle. Conversely, if the lengths of perpendiculars from the center of the circle to two chords are equal, the chords are equal.
3. The length of a chord keeps increasing as it moves closer to the center of the circle, diameter being the largest chord

Inscribed angle Theorem : The angle inscribed by the two points lying on the circle, at the centre of the circle is twice the angle inscribed at any point on the circle by the same points:

Angles subtended by the same segment on the circle will be equal. So here angles a and b will be equal:

Equal Chords subtend equal angles at the centre 

The angle subtended by a diameter on the circumference is a right angle

• Consider a circle as shown in the image. Here, $$AP$$ * $$AQ$$ = $$AS$$ * $$AU$$ = $$AT^2$$

• Two tangents drawn to a circle from an external common point will be equal in length. So here AZ = AT
• Two chords that are equal in length will be equidistant from the centre and vice versa.
• When two circles intersect, the line joining the centres perpendicularly bisects the line joining the points of intersection.
  
• Alternate Segment Theorem:
• The angle made by a chord with a tangent to one of the ends of the chord is equal to the angle subtended by the chord in the other segment. As shown in the figure, angle ACB = angle BAT.

Tangents:

Direct common tangent: $$PQ^2=RS^2=D^2-\left(r_1-r_2\right)^2$$, where D is the distance between the centres:

Transverse common tangent: $$PQ^2=RS^2=D^2-\left(r_1+r_2\right)^2$$, where D is the distance between the centres:

• Consider the triangle ABC with incentre I, and the incircle touching the triangle at P,Q,R as shown in the diagram. As tangents drawn from a point are equal, AP=AQ, CP=CR and BQ=BR.

• In an equilateral triangle, the centroid divides the median in the ratio 2:1. As the median is also the perpendicular bisector, angle bisector, G is also the circumcentre and incentre.
• If a is the side of an equilateral triangle, circumradius = $$ a/\sqrt{3}$$ and inradius = $$ = a/2\sqrt{3}$$.
• if a is the side of a triangle opposite to angle A, circumradius = $$\dfrac{a}{2\sin A}$$
• Area = s * r where s is the semi-perimeter and r is the in-radius.

If a quadrilateral has all its vertices on the circle and its opposite angles are supplementary (here x+y = 180^{0}), then that quadrilateral is called a cyclic quadrilateral.

• In a cyclic quadrilateral, the opposite angles are supplementary
• Area of a cyclic quadrilateral is $$A$$ = $$\sqrt{(s-a)(s-b)(s-c)(s-d)} $$ where s=(a+b+c+d)/2
• The exterior angle is equal to the opposite angle of its remote interior interior. (here ∠CBX = ∠ADC)
• A = 1/2 * One diagonal * Sum of offsets drawn to the diagonal
• Ptolemy's theorem states that the product of the diagonals equals the sum of the products of the opposite sides. AC*BD = AB*CD + AD*BC.
• For a trapezium, Area = 1/2 * sum of parallel sides * distance between them
• For a parallelogram, A=Base * Height = Product of two sides * sine of the included angle
• For a rhombus = 1/2 * Product of diagonals
• For any solid, Euler's rule states that The number of faces + Number of vertices = Number of edges +2
• The sum of the three sides of a quadrilateral must be greater than the fourth side.

Polygons:

▪ If all sides and all angles are equal, then the polygon is a regular polygon
▪ A regular polygon of n sides has n(n-3)/2 diagonals
▪ In a regular polygon of n sides, each exterior angle is 360/n degrees.
▪ Sum of measure of all the interior angles of a regular polygon is 180 (n-2)
degrees (where n is the number of sides of the polygon)
▪ Sum of measure of all the exterior angles of regular polygon is 360 degrees

ABCDEF is a regular hexagon with each side equal to ‘x’ then

▪ Each interior angle = 120 degrees

▪ Each exterior angle = 60 degrees

▪ Sum of all the exterior angles = 360 degrees

▪ Sum of all the interior angles = 720 degrees

▪ Area = $$\frac{3\sqrt{\ 3}}{2}a^2$$.

- Quadrilateral with only one pair of opposite sides are parallel.

- Area = $$\dfrac{1}{2}\times\ height\ \times\ \left(Sum\ of\ parallel\ sides\right)$$ i.e. If h is the height and AB, CD are the opposite parallel sides, then Area = $$\dfrac{1}{2}\times h\times\left(AB+CD\right)$$

If the vertices of the triangle are $$A\ \left(x_1,y_1\right),\ B\left(x_2,y_2\right)\ \&\ C\left(x_3,y_3\right)$$ and the lengths of the sides BC, CA and AB are a, b, c, respectively

then, 

•  Coordinates of the centroid (G) are: $$\left(\frac{\left(x_1+x_2+x_3\right)}{3},\frac{\left(y_1+y_2+y_3\right)}{3}\right)$$
• Coordinates of the Incenter (I) are:  $$\left(\frac{ax_1+bx_2+cx_3}{a+b+c},\frac{ay_1+by_2+cy_3}{a+b+c}\right)$$

If 'p' is the given perimeter,

The total number of triangles

= $$\dfrac{p^2}{48}$$ if p is even

= $$\dfrac{\left(p+3\right)^2}{48}$$ if p is odd

The number of scalene triangles

= $$\dfrac{\left(p-6\right)^2}{48}$$ if p is even

= $$\frac{\left(p-3\right)^2}{48}$$ if p is odd

In all the cases, the value obtained should be rounded to the nearest integer.

In a right-angled triangle, we consider an angle 'x'

Sin(x) = $$\dfrac{opposite}{hypotenuse}$$

Cos(x) = $$\dfrac{adjacent}{hypotenuse}$$

Tan(x) = $$\dfrac{opposite}{adjacent}$$

Trigonometric values for important angles: 0. 30, 45, 60, 90.

Sin(0) = 0, Sin(30) = 1/2, Sin(45) = 1/$$\sqrt{\ 2\pm\ }$$, sin(60) = $$\frac{\sqrt{\ 3}}{2}$$, sin(90) = 1

Cos(0) = 1, Cos(30) = $$\frac{\sqrt{\ 3}}{2}$$, cos(45) = 1/$$\sqrt{\ 2\pm\ }$$, cos(60) = Sin(30) = 1/2, cos(90) = 0

Tan(0) = 0, Tan(30) = $$\frac{1}{\sqrt{\ 3}}$$, Tan(45) = 1, Tan(60) = $$\sqrt{\ 3}$$, Tan(90) = infinity.

Sin(90+x) = cos(x)

Cos(90+x) = -sin(x)

sin(-x) = -sin(x)

cos(-x) = cos(x)

$$\sin^2\left(x\right)+\cos^2\left(x\right)=1$$

sin(x+y) = sin(x)cos(y) + cos(x)sin(y)

cos(x+y) = cos(x)cos(y) - sin(x)sin(y)

- A line joining the midpoint of a side with the opposite vertex is called a Median.

- The point of intersection of the three medians is the Centroid.

- A perpendicular drawn from a vertex to the opposite side is called the Altitude.

-The three perpendicular bisectors of a triangle meet at a point called the Circumcentre.

- A circle drawn from this point with the circumradius would pass through all the vertices of the triangle.

- The three angle bisectors of a triangle meet at a point called the incentre of a triangle.

- The incentre is equidistant from the three sides, and a circle drawn from this point with the inradius would touch all the sides of the triangle.

- The point of intersection of the three altitudes is the Orthocentre.

• If h, k represents the coordinates of the circle, and r represents the length of the radius of the circle, the equation of the circle is $$\left(x-h\right)^2+\left(y-k\right)^2=r^2$$

• Equation of the circle if the origin is the centre of the circle = $$x^2+y^2=r^2$$

- The Sum of all angles in a triangle is 180 degrees.

- An angle less than 90 degrees is called an acute angle.

- An angle greater than 90 degrees is called an Obtuse angle.

- The Sum of any two sides of a triangle is always greater than the third side.

- A triangle with two sides equal is called an Isosceles triangle

- A triangle with all sides equal is called an equilateral triangle.

- A triangle with all sides unequal is called a scalene triangle.

Characteristics of the four quadrants:

• Quadrant I: X is Positive, Y is Positive
  Quadrant II: X is Negative, Y is Positive
  Quadrant III: X is Negative, Y is Negative
  Quadrant IV :X is Positive, Y is Negative

Volume of Tetrahedron of side 'a' = $$\dfrac{a^3}{6\sqrt{\ 2}}$$

Coordinate geometry formulae:

• The distance between two points with coordinates $$(x_1, y_1), (x_2, y_2)$$ is given by $$ d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
• Point slope form of the equation of a line is $$y-y_1=m(x-x_1)$$
• Two point form of the equation of a line is $$y-y_1=(y_2-y_1)\left(\frac{x-x_1}{x_2-x_1}\right)$$
  
• Mid point between two points $$A\left(x_1,y_1\right)$$ and $$B\left(x_2,y_2\right)$$ is $$\left(\frac{\left(x_1+x_2\right)}{2},\frac{\left(y_1+y_2\right)}{2}\right)$$
• Coordinates of a point P that divides the line joining $$A\left(x_1,y_1\right)$$ and $$B\left(x_2,y_2\right)$$ internally in the ratio l:m : $$\left(\frac{\left(lx_2+mx_1\right)}{l+m},\frac{\left(ly_2+my_1\right)}{l+m}\right)$$.
• Coordinates of a point P that divides the line joining $$A\left(x_1,y_1\right)$$ and $$B\left(x_2,y_2\right)$$ externally in the ratio l:m : $$\left(\frac{\left(lx_2-mx_1\right)}{l-m},\frac{\left(ly_2-my_1\right)}{l-m}\right)$$.
• A line can be defined as $$y=mx+c$$ where m is the slope of the line and c is the y-intercept.
• Slope $$m=\frac{\left(y_2-y_1\right)}{x_2-x_1}$$. Here, if $$x_2=x_1$$, then the two lines are perpendicular to each other.
• When two lines are parallel, their slopes are equal i.e $$m_1=m_2$$
• When two lines are perpendicular, product of their slopes = -1 i.e $$m_1*m_2=-1$$
• If a and b are the x and y intercept of a line then $$\frac{x}{a}+\frac{y}{b}=1$$
• If two intersecting lines have slopes $$m_1$$ and $$m_2$$, then the angle between the two lines will be $$\tan\theta\ =\frac{\left(m_1-m_2\right)}{1+m_1m_2}$$.
• The length of perpendicular from a point $$\left(X_1,Y_1\right)$$ on the line AX+BY+C=0 is $$\frac{\left(AX_1+BY_1+C\right)}{\sqrt{\ A^2+B^2}}$$.
• The distance between two parallel lines Ax+By+C1 = 0 and Ax+By+C2= 0 is $$\left|\frac{C_1-C_2}{\sqrt{\ A^2+B^2}}\right|$$
• Image of the point (m,n) in the line ax + by + c = 0 is given by $$\dfrac{\left(x-m\right)}{a}=\dfrac{\left(y-n\right)}{b}=-\dfrac{2\left(am+bn+c\right)}{a^2+b^2}$$
• 2. To find the number of integral points inside the closed area, we can use Pick's Theorem. 
• Pick's Theorem: $$A\ =\ I+\frac{B}{2}-1$$ (Where, A = Area of the closed figure, I = the number of points inside the figure, B = the number of points on the boundaries)

• The general equation of a circle is $$x^2+y^2+2gx+2fy+c=0$$. Here, the centre of the circle is (-g,-f); the radius of the circle is $$\sqrt{\ g^2+f^2-c}$$.
  
• If the centre of the circle lies on the origin, the equation is $$x^2+y^2=r^2$$, where r is the radius of the circle.
• For a triangle ABC, A (x₁, y₁), B (x₂, y₂), C (x₃, y₃):
  • Centroid= $$\left(\frac{\left(x_1+x_2+x_3\right)}{3},\frac{y_1+y_2+y_3}{3}\right)$$
  • Incentre= $$\left(\frac{\left(ax_1+bx_2+cx_3\right)}{a+b+c},\frac{ay_1+by_2+cy_3}{a+b+c}\right)$$ ;where a, b and c are the lengths of the BC, AC and AB respectively.