Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 69
AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to
Solution
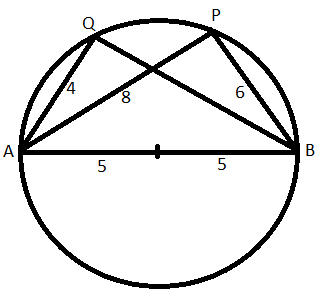
Since AB is a diameter, AQB and APB will right angles.
In right triangle APB, AP = $$\sqrt{10^2-6^2}=8$$
Now, 2AQ=AP => AQ= 8/2=4
In right triangle AQB, AP = $$\sqrt{10^2-4^2}=9.165$$ =9.1 (Approx)
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
CAT Quant Questions | CAT Quantitative Ability
CAT Linear Equations QuestionsCAT Mensuration QuestionsCAT Time And Work QuestionsCAT Logarithms QuestionsCAT Percentages Questions
CAT DILR Questions | LRDI Questions For CAT
CAT Venn Diagrams QuestionsCAT Puzzles QuestionsCAT Games and Tournamnents QuestionsCAT Data Interpretation QuestionsCAT Truth Lie Concept Questions
