In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is

Given that two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm.

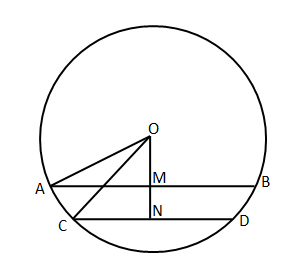
In the diagram we can see that AB = 6 cm, CD = 4 cm and MN = 1 cm.

We can see that M and N are the mid points of AB and CD respectively. 

AM = 3 cm and CD = 2 cm. Let 'OM' be x cm. 

In right angle triangle AMO,

$$AO^2 = AM^2 + OM^2$$ 

$$\Rightarrow$$ $$AO^2 = 3^2 + x^2$$  ... (1)

In right angle triangle CNO,

$$CO^2 = CN^2 + ON^2$$ 

$$\Rightarrow$$ $$CO^2 = 2^2 + (OM+MN)^2$$ 

$$\Rightarrow$$ $$CO^2 = 2^2 + (x+1)^2$$  ... (2)

We know that both AO and CO are the radius of the circle. Hence $$AO = CO$$

Therefore, we can equate equation (1) and (2)

$$3^2+x^2$$=$$2^2+(x+1)^2$$

$$\Rightarrow$$ x = 2 cm

Therefore, the radius of the circle 

$$AO = \sqrt{AM^2 + OM^2}$$ 

$$\Rightarrow$$ $$AO=\sqrt{3^2+2^2}=\sqrt{13}$$. Hence, option A is the correct answer.