Question 64

Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is

Name: Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is
Uploaded: May 3, 2022, 4:31 p.m.
Duration: 2 min 38 s
Description: Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is

Correct Answer: 30

Solution

We have :

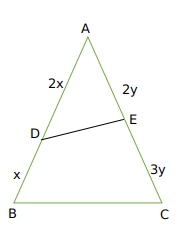
Now area of ADE = $$\frac{1}{2}\times\ AD\times\ AE\times\ \sin A$$
=$$\frac{1}{2}\times\ 2x\times\ 2y\times\ \sin A=8$$
we get xy sinA =4
Now Area of triangle ABC = $$\frac{1}{2}AB\times\ AC\times\ \sin A$$
we get $$\frac{1}{2}\times3x\ \times5y\ \sin A=\frac{15}{2}xy\ \sin A=\ \frac{15}{2}\times\ 4$$
we get Area of ABC = 30

Video Solution

Click on the Email ☝️ to Watch the Video Solution

Create a FREE account and get:

All Quant CAT complete Formulas and shortcuts PDF
35+ CAT previous papers with video solutions PDF
5000+ Topic-wise Previous year CAT Solved Questions for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Progressions and Series Questions CAT Profit, Loss and Interest Questions CAT Algebra Questions CAT Averages Mixtures Alligations Questions CAT Percentages Questions

CAT DILR Questions | LRDI Questions For CAT

CAT DI with connected data sets Questions CAT Games and Tournamnents Questions CAT Venn Diagrams Questions CAT Quant Based LR Questions CAT Special Charts Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Odd One Out Questions CAT Vocabulary Questions CAT Para Summary Questions CAT Reading Comprehension Questions CAT Grammar and Sentence Correction Questions

Related Formulas With Tests

Triangle - Area

CAT 2021 QA Slot 2 Question

Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is

Video Solution

CAT Quant Questions | CAT Quantitative Ability

CAT DILR Questions | LRDI Questions For CAT

CAT Verbal Ability Questions | VARC Questions For CAT

Free Quant Questions

Related Formulas With Tests

Login to your Cracku account

Hello! 👋

Ready to Unlock Your Success?

Please Enter Your OTP

Please enter the following details

Create a free Cracku account