Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 60
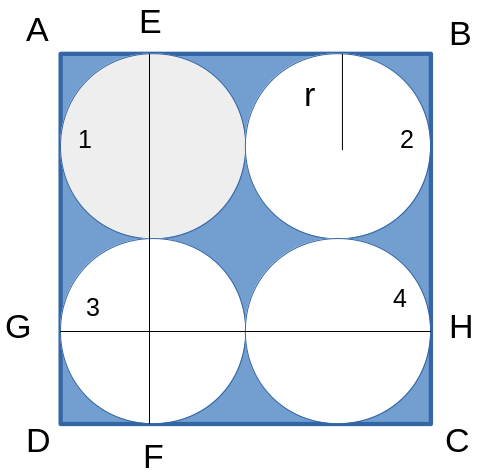
Four identical coins are placed in a square. For each coin the ratio of area to circumference is same as the ratio of circumference to area. Then find the area of the square that is not covered by the coins.
Solution
$$\frac{(\pi r^2)}{2 \pi r}$$ =Â $$\frac{2 \pi r}{ \pi r^2}$$
So r = 2
Hence required area = (Area of square) - (Area of 4 circles)
= $$(8^2) - (4 \pi (2^2))$$ (As side of square will be 4*2 = 8)
= $$16 (4- \pi)$$
The intended diagram can be drawn as follows:
ABCD is the square and the coins are placed (numbered 1,2,3,4)
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
CAT Quant Questions | CAT Quantitative Ability
CAT Time, Distance and Work QuestionsCAT Number Series QuestionsCAT Averages QuestionsCAT Arithmetic QuestionsCAT Remainders Questions
CAT DILR Questions | LRDI Questions For CAT
CAT Routes And Networks QuestionsCAT Scheduling QuestionsCAT Table with Missing values QuestionsCAT Special Charts QuestionsCAT Data Interpretation Questions
