Question 55

The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

Name: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is
Uploaded: May 3, 2022, 4:31 p.m.
Duration: 2 min 12 s
Description: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

Solution

We are given that :

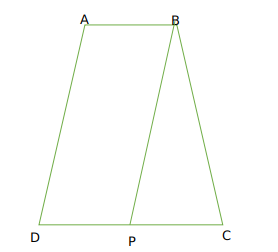
Let DP =x
So AB =x
Now DP=CP
So CD = 2x
Now let height of trapezium be h
we can say A(Parallelogram ABPD ) = xh
And A (BPC) =$$\frac{1}{2}xh$$
Now by condition$$xh-\frac{1}{2}xh=10$$
$$\frac{xh}{2}=10$$
so xh =20
Now therefore area of trapezium ABCD = $$\frac{1}{2}\left(x+2x\right)h\ =\ \frac{3}{2}xh\ =\ 30$$

Share on Whatsapp Share on Whatsapp

Boost your CAT prep: Take All-India 3 free CAT mock tests with Video solutions

Video Solution

Click on the Email ☝️ to Watch the Video Solution

Create a FREE account and get:

All Quant CAT complete Formulas and shortcuts PDF
35+ CAT previous year papers with video solutions PDF
5000+ Topic-wise Previous year CAT Solved Questions for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Averages Mixtures Alligations Questions CAT Coordinate Geometry Questions CAT Functions, Graphs and Statistics Questions CAT Probability, Combinatorics Questions CAT Time Speed Distance Questions

CAT DILR Questions | LRDI Questions For CAT

CAT Quant Based LR Questions CAT Arrangement Questions CAT Quant Based DI Questions CAT Puzzles Questions CAT DI Miscellaneous Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Para Jumbles Questions CAT Critical Reasoning Questions CAT Miscellaneous Questions CAT Verbal Ability Questions CAT Para Summary Questions

The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

Video Solution

CAT Quant Questions | CAT Quantitative Ability

CAT DILR Questions | LRDI Questions For CAT

CAT Verbal Ability Questions | VARC Questions For CAT

Also Read

Related Formulas With Tests

CAT 2021 QA Slot 2 Question

The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

Video Solution

CAT Quant Questions | CAT Quantitative Ability

CAT DILR Questions | LRDI Questions For CAT

CAT Verbal Ability Questions | VARC Questions For CAT

Also Read

Free CAT Quant Questions

Related Formulas With Tests

Login to your Cracku account

Hello! 👋

Ready to Unlock Your Success?

Please Enter Your OTP

Please enter the following details

Create a free Cracku account

Get Started with 5000+ Free CAT Questions & Mock Tests with Detailed Solutions!