Sign in
Please select an account to continue using cracku.in
↓ →
Read the following scenario and answer the THREE questions that follow.
Comprehension:
The diagram below represents a road network connecting five towns, namely Meereen, Lannisport, Winterfell, Oldtown, and Gulltown. The maximum speed limits along any stretch of road are as shown in the diagram. The straight road that connects Meereen to Gulltown passes through Oldtown. Another straight road, running west to east, connecting Meereen to Winterfell, passes through Lannisport. Further, two straight roads, one from Lannisport to Oldtown and another from Winterfell to Gulltown, are perpendicular to the road joining Meereen to Winterfell, and run from south to north.
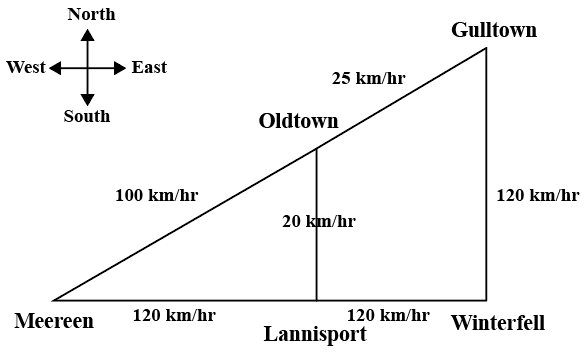
Consider a car always travelling at the maximum permissible speed, and always taking the shortest route. It takes 1 hour to reach Oldtown from Meereen, 2 hours to reach Gulltown from Oldtown, and 45 minutes to reach Winterfell from Gulltown. (For this problem, always consider the shortest route in terms of distance.)
The capital city, King’s Landing, located 40 km to the south of Gulltown on the road connecting Gulltown to Winterfell, did not have a straight road, connecting to Meereen. Now, a new expressway is being built to connect these two towns by a straight road.
What should be the maximum speed limit allowed on this expressway so that it cuts down the travel time, from Meeren to King’s Landing, from the fastest possible route through the road network shown in the diagram, by 20 minutes?
We are told that a car always travelling at the maximum permissible speed, and always taking the shortest route takes 1 hour to reach Oldtown from Meereen, 2 hours to reach Gulltown from Oldtown, and 45 minutes to reach Winterfell from Gulltown.
So, distance between Oldtown and Meereen is 100*1 = 100km
Distance between Gulltown and Oldtown is 25*2 = 50km.
Distance between Winterfell and Gulltown. Is 120*3/4 = 90km.
Let the distance between Meereen and Winterfall be x.
Using the Pythagoras theorem, $$(100+50)^2=90^2+x^2$$
x = 120 km
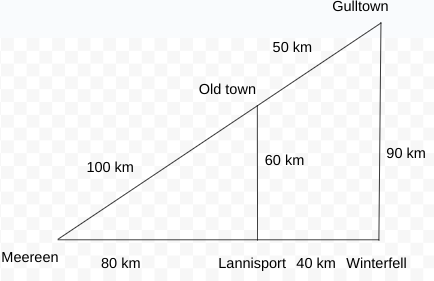
For convenience, we are referring to the vertices as the starting letters of towns.
Using the similar triangle rule, MOL is similar to MGW.
So, $$\frac{MO}{ML}=\frac{MG}{MW}$$
$$\frac{100}{ML}=\frac{150}{120}$$
ML = 80 km.
LW = 40 km.
$$\frac{MO}{LO}=\frac{MG}{WG}$$
$$\frac{100}{LO}=\frac{150}{90}$$
LO = 60 km
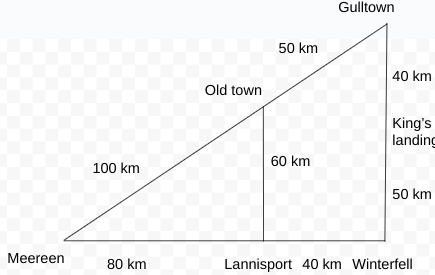
The direct path from M to K will be $$\sqrt{\ 120^2+50^2}=\ 130\ km$$.
Time taken for the path MOGK,= $$\frac{100}{100}+\frac{50}{25}+\frac{40}{120}\ =1+2+\frac{1}{3}=3.33$$
Time taken for the path MWK = $$\frac{120}{120}+\frac{50}{120}\ =1.42$$
So, the second case is MWK, which is the fastest route. The time taken will be 1 hr 25 mins.
If the travel time is cut down by 20 mins, the new time will be 1 hr 5 mins. So, it should take 13/12 hrs.
speed = $$\dfrac{130}{\frac{13}{12}}=120 kmph$$
Create a FREE account and get:
Educational materials for CAT preparation