Read the following scenario and answer the THREE questions that follow.
Comprehension:
The diagram below represents a road network connecting five towns, namely Meereen, Lannisport, Winterfell, Oldtown, and Gulltown. The maximum speed limits along any stretch of road are as shown in the diagram. The straight road that connects Meereen to Gulltown passes through Oldtown. Another straight road, running west to east, connecting Meereen to Winterfell, passes through Lannisport. Further, two straight roads, one from Lannisport to Oldtown and another from Winterfell to Gulltown, are perpendicular to the road joining Meereen to Winterfell, and run from south to north.
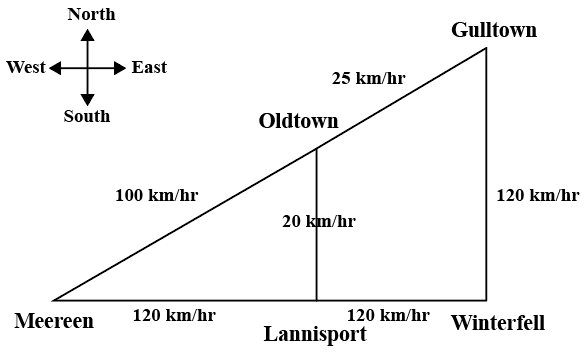
Consider a car always travelling at the maximum permissible speed, and always taking the shortest route. It takes 1 hour to reach Oldtown from Meereen, 2 hours to reach Gulltown from Oldtown, and 45 minutes to reach Winterfell from Gulltown. (For this problem, always consider the shortest route in terms of distance.)
Missandei starts from Gulltown towards Oldtown by the shortest path, driving at the maximum permissible speed. From Oldtown, she drives at a speed of 10 km/hr towards Lannisport. When Missandei starts from Gulltown, Varys starts at the same time from Lannisport to Oldtown along the shortest path, always driving at the maximum permissible speed.
If they don’t stop anywhere, at what point will they meet?
Solution
We are told that a car always travelling at the maximum permissible speed, and always taking the shortest route takes 1 hour to reach Oldtown from Meereen, 2 hours to reach Gulltown from Oldtown, and 45 minutes to reach Winterfell from Gulltown.
So, distance between Oldtown and Meereen is 100*1 = 100km
Distance between Gulltown and Oldtown is 25*2 = 50km.
Distance between Winterfell and Gulltown. is 120*3/4 = 90km.
Let the distance between Meereen and Winterfall be x.
Using the pythagoras theorem, $$(100+50)^2=90^2+x^2$$
x = 120 km
For convience, we are refering the vertices as the starting letters of towns.
Using the similar triangle rule, MOL is similar to MGW.
So, $$\frac{MO}{ML}=\frac{MG}{MW}$$
$$\frac{100}{ML}=\frac{150}{120}$$
ML = 80 km.
LW = 40 km.
$$\frac{MO}{LO}=\frac{MG}{WG}$$
$$\frac{100}{LO}=\frac{150}{90}$$
LO = 60 km
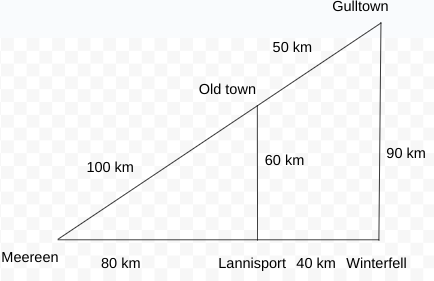
The path taken by Missandei is GO, OL at a speed of 25 kmph and 10 kmph. The path taken by Varys is LO at a speed of 20 kmph.
Missandei reaches O 2 hours after he starts. In the meantime, Varys travels 20 * 2 = 40km.
Now, both are travelling in opposite directions and 20 km away.
The speed of Varys is 20 kmph, and that of Missandei is 10 kmph.
The time taken for them to meet is 20/30 = 2/3 hr.
In 2/3 hr, Missandei travels 6.67 km, and Varys travels 13.33 km.
So, they will meet at 6.67 km south of Oldtown.
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
