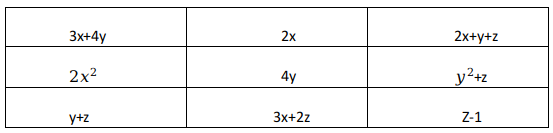
Rahul has just made a $$3 \times 3$$ magic square, in which, the sum of the cells along any row, column or diagonal, is the same number N. The entries in the cells are given as expressions in x, y, and Z. Find N?
Solution
Sum of 3rd row = sum of 2nd column
=> 2x+4y = y+2z-1
=> 2x+3y-2z= -1 ------- (A)
Sum of diagonals are also equal
=> 3x+4y+z-1 = y+z+2x+y+z
=> x+2y-z=1 -----(B)
Solving A and B we get y= 3
Putting it in A, we get x-z = -5 ----- (C)
Sum of 1st row = sum of 2nd column
5x+5y+z = 3x+4y+2z
=> 2x +y - z =0
Since y=3, 2x-z = -3 ------ (D)
Solving C and D we get x=2 and z=7
Hence N = 36
Get AI Help
Video Solution
Click on the Email ☝️ to Watch the Video Solution
XAT Quant Questions | XAT Quantitative Ability
XAT DILR Questions | LRDI Questions For XAT
XAT Verbal Ability Questions | VARC Questions For XAT
Free XAT Quant Questions
Related Formulas With Tests
Book Free CAT Mentorship
Get personalized CAT strategy from a 99%iler
500+ students mentored
OTP Verification
Enter the 6-digit code sent to your phone
Booking Summary
Enter OTP
Didn't receive the OTP?
