SRCC GBO 2011 Question Paper
For the following questions answer them individually
SRCC GBO 2011 - Question 61
If x and y are positive numbers, the largest of the following is
SRCC GBO 2011 - Question 62
A book has 213 problemsfrom 12 years, of competitions. At first there were 25 problems per year, then 16 problems per year and finally 20 problems per year. The number of years when there were 25 problems was
SRCC GBO 2011 - Question 63
The ratio of the maximum value and the minimum value of $$\sin^6 x + \cos^6 x$$ is
SRCC GBO 2011 - Question 64
Let a = 111....1 (where the number of 1's is m) be an integer and b = 100....05 (where the number 0's is m - 1), then $$\sqrt{ab + 1} =$$
SRCC GBO 2011 - Question 65
If $$(\log_3 x)(\log_x 2x)(\log_{2x} y) = \log_x x^2$$, then y equals
SRCC GBO 2011 - Question 66
Parallel lines are drawn on a rectangular piece of paper, The paper is then cut along each of, the lines, forming n identical rectangular strips. If the strips have the same ratio of length to width as the original paper, this ratio is
SRCC GBO 2011 - Question 67
In the figure, ABCD is a rectangle and each circle has diameter 4 cm. The length BC is equal to
.png)
SRCC GBO 2011 - Question 68
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is $$5\sqrt{5}$$ cm. Its surface area is
SRCC GBO 2011 - Question 69
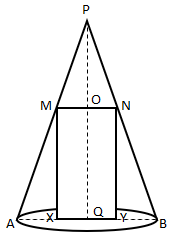
A right circular cylinder with its diameter equal to its height is incribed in a right circular cone. The base radius and altitude of the cone are 5 cm and 12 cm respectively, and axes of cylinder and cone consider the diameter of the cylinder is
SRCC GBO 2011 - Question 70
A shopkeeper buys goods at 25% off the list price. He desires to mark the goods so that he can give a discount of 20% on the marked price and still have a psofit of 25% on the selling price. What percent of the list price, must be marked on the goods ?