Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 69
A right circular cylinder with its diameter equal to its height is incribed in a right circular cone. The base radius and altitude of the cone are 5 cm and 12 cm respectively, and axes of cylinder and cone consider the diameter of the cylinder is
Solution
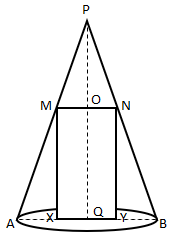
Base radius of cone = AQ = BQ = 5 cm
AB = 2AQ = 10 cm
Height of cone = PQ = 12 cm
Let QY = x and OQ = 2x
MN = XY = 2x
Now,
$$\frac{MN}{AB} = \frac{PO}{PQ}$$
$$\frac{2x}{10} = \frac{12 - 2x}{12}$$
6x = 30 - 5x
$$x = \frac{30}{11}$$
Ddiameter of the cylinder = XY = 2x = $$\frac{60}{11} cm$$
