In a circle with center O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is

It is given that radius of the circle = 1 cm

Chord AB subtends an angle of 60° on the centre of the given circle. R be the region bounded by the radii OA, OB and the arc AB.

Therefore, R = $$\dfrac{60°}{360°}$$*Area of the circle = $$\dfrac{1}{6}$$*$$\pi*(1)^2$$ = $$\dfrac{\pi}{6}$$ sq. cm

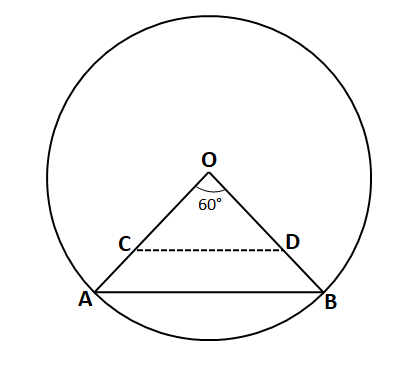
It is given that OC = OD and area of triangle OCD is half that of R. Let OC = OD = x.

Area of triangle COD = $$\dfrac{1}{2}*OC*OD*sin60°$$

$$\dfrac{\pi}{6*2}$$ = $$\dfrac{1}{2}*x*x*\dfrac{\sqrt{3}}{2}$$

$$\Rightarrow$$ $$x^2 = \dfrac{\pi}{3\sqrt{3}}$$

$$\Rightarrow$$ $$x$$ = $$(\frac{\pi}{3\sqrt{3}})^{\frac{1}{2}}$$ cm. Hence, option C is the correct answer.