The swimming pool in an exclusive club is a circular strip. A water flow is artificially maintained in the strip, along a clockwise direction, at a constant speed of 3km/h (kilometers/hour). One morning, Ayub and Rana start swimming at the same time from two diametrically opposite points on the strip. Ayub swims in a counterclockwise direction, while Rana swims in a clockwise direction. They swim at constant, but different, speeds. When they meet for the first time, Ayub has covered 60m (meters). They meet again after Rana has covered 180m from the first meeting point.
If Rana swims at the speed of 3 km/h in still water, how long does Ayub take to complete one round of the circular strip, if he swims in the clockwise direction?

Let us denote Ayub and Rana as A and R respectively for simplicity. 

Let the speed of A and B in still water be Sa and Sr respectively and the speed of river be r. 

r = 3 kmph = 50 $$\ \frac{\ m}{\min}$$ (clockwise)

Sr = 3 kmph = 50 $$\ \frac{\ m}{\min}$$ (clockwise)

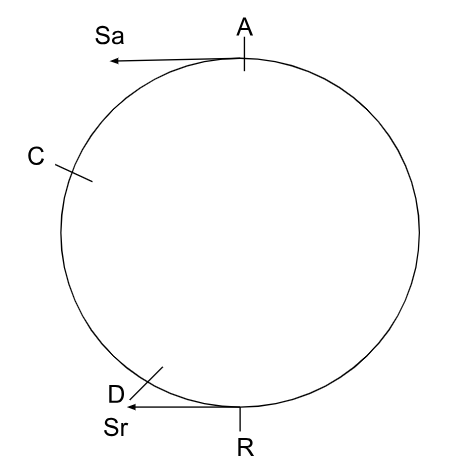
Since A is swimming in counter clockwise direction and R is swimming in clockwise direction, let C be the point where they meet for the first time. 

Distance travelled by A = AC = 60m 

Speed of A = (Sa-50) $$\ \frac{\ m}{\min}$$ (as he is travelling in counter clockwise direction which is upstream)

Time taken by A to reach C = $$\ \frac{\ 60}{Sa-50}\min$$

Speed of R = (Sr+50) $$\ \frac{\ m}{\min}$$ (as he is travelling in clockwise direction which is downstream)

= 100 $$\ \frac{\ m}{\min}$$

Since, the time taken by R to reach C is the same as the time taken by A to reach C (as they started swimming at the same time), distance travelled by R = RC = $$\ \frac{\ 100\times\ 60}{Sa-50}m$$

Total distance travelled by both A and R = AC + RC = $$\ \frac{\ 6000}{Sa-50}+60\ m$$

As A and R travelled in opposite directions from exactly diametrical ends, the distance A to R will be half of the circumference of the circle. 

$$\pi\ r$$ = $$\ \frac{\ 6000}{Sa-50}+60\ m$$ $$\longrightarrow\ i$$

Now, let's assume that they meet again at D after R travelled for 180m, 

Time taken for them to meet again = $$\ \frac{\ 180}{100}\min$$

Distance travelled by A = CD (in counter clockwise direction) = $$\ \frac{\ \left(Sa-50\right)\times\ 180}{100}m$$

Distance travelled by R = CD (in clockwise direction) = 180m 

Total distance travelled = $$\ \frac{\ \left(Sa-50\right)\times\ 180}{100}m$$ + 180 m

This distance will be equal to the circumference of the circle. 

Hence, $$2\pi\ r$$ = $$\ \frac{\ \left(Sa-50\right)\times\ 180}{100}m$$ + 180 m $$\longrightarrow\ ii$$

Take the value of $$\pi\ r$$ from equation i and substitute it in equation ii. 

$$\ \frac{\ 12000}{Sa-50}+120=\ \frac{\ 180\left(Sa-50\right)}{100}+180$$

Let the value of Sa-50 be t.

 $$\ \frac{\ 12000}{t}+120=\ \frac{\ 180\left(t\right)}{100}+180$$

$$\ 3t^2+100t-20000=0$$

t = $$\ \frac{\ 200}{3}$$, -100 (Not possible as the speed can't be negative)

Sa-50 = $$\ \frac{\ 200}{3}$$

Sa = $$\ \frac{\ 350}{3}\ \frac{\ m}{\min}$$

Use this value in equation ii to get, $$2\pi\ r$$ = 300m

Speed of A when he is swimming in clockwise direction = $$\ \frac{\ 350}{3}+50$$

= $$\ \frac{\ 500}{3}\ \frac{\ m}{\min}$$

Time taken by A to complete one round of the circular strip = $$\ \frac{300}{\ \frac{\ 500}{3}\ }\min$$

= $$\ \frac{\ 9}{5}\min$$ = 1 min 48 sec

Hence, the time taken by A to complete one round of the circular strip is 1 min 48 sec. 

$$\therefore\ $$ The answer is D.