Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be

We can see that T$$_{2}$$ is formed by using the mid points of T$$_{1}$$. Hence, we can say that area of triangle of T$$_{2}$$ will be (1/4)th of the area of triangle T$$_{1}$$.

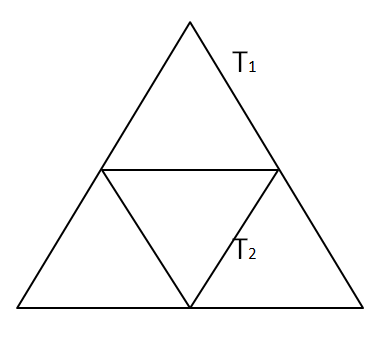
Area of triangle T$$_{1}$$ = $$\dfrac{\sqrt{3}}{4}*(24)^2$$ = $$144\sqrt{3}$$ sq. cm

Area of triangle T$$_{2}$$ = $$\dfrac{144\sqrt{3}}{4}$$ = $$36\sqrt{3}$$ sq. cm 

Sum of the area of all triangles =  T$$_{1}$$ + T$$_{2}$$ + T$$_{3}$$ + ... 

$$\Rightarrow$$ T$$_{1}$$ + T$$_{1}$$/$$4$$ + T$$_{1}$$/$$4^2$$ + ... 

$$\Rightarrow$$ $$\dfrac{T_{1}}{1 - 0.25}$$

$$\Rightarrow$$ $$\dfrac{4}{3}*T_{1}$$

$$\Rightarrow$$ $$\dfrac{4}{3}*144\sqrt{3}$$

$$\Rightarrow$$ $$192\sqrt{3}$$

Hence, option D is the correct answer.