Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?

Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?

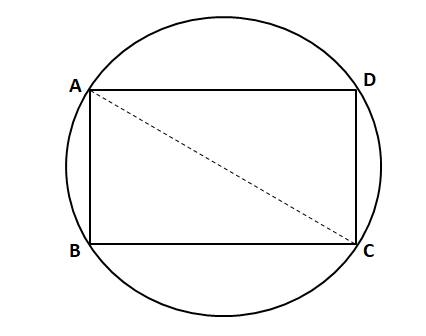
We know that AC is the diameter and $$\angle$$ ABC = 90°. AC = 2*13 = 26 cm

In right angle triangle ABC,

$$AC^2 = AB^2 + BC^2$$

$$\Rightarrow$$ $$AB^2+BC^2=26^2$$

$$\Rightarrow$$ $$AB^2+BC^2=676$$

Let us check with the options.

Option (A): $$24^2+10^2 = 676$$. Hence, this is a possible answer. 

Option (B): $$25^2+9^2 = 706 \neq 676$$.  Hence, this is an incorrect pair.

Option (C): $$25^2+10^2 = 725 \neq 676$$.  Hence, this is an incorrect pair.

Option (D): $$24^2+12^2 = 720 \neq 676$$. Hence, this is an incorrect pair.

Therefore, we can say that option A is the correct answer.