Read the following scenario and answer the THREE questions that follow.
A pencil maker ships pencils in boxes of size 50, 100 and 200. Due to packaging issues, some pencils break. About the 20 boxes he has supplied to a shop, the following information is available:
* Box no. 1 through 6 have 50 pencils, Box no. 7 through 16 have 100 pencils and Box no. 17 through 20 have 200 pencils.
* No box has less than 5% or more than 20% broken pencils.
Following is the frequency table of the number of broken pencils for the twenty boxes:
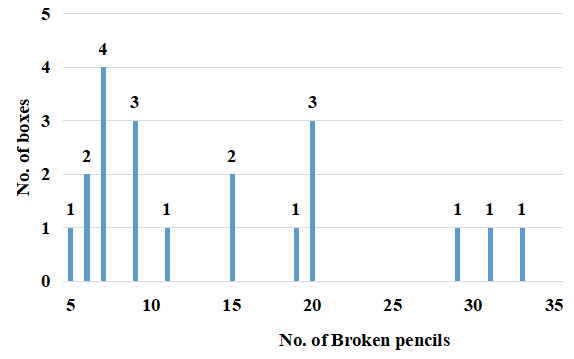
Suppose that additionally it is known that the number of broken pencils in Boxes 17-20 are in increasing order. Which among the following additional information, if true, is not sufficient to uniquely know the number of defective pencils in each of the boxes numbered 17-20?
Going by the options :
Option A: Boxes 7- 16 contain a total of 124 pencils. Boxes (1-6) has 6 boxes with broken pencils which can be included from :
(5, 6, 6, 7, 7, 7, 7, 9, 9, 9). The minimum possible sum of the 6 pencils is : (5+6+6+7) = 24 and the maximum possible sum is (7+9+9+9) = 34.
Boxes 7 - 16 contains all the boxes with broken pencils except one among the boxes with broken pencils among 11 - 20 and hence ;
This can contain : (11+15+15+19+20+20) or (15+15+19+20+20+20) or (11+15+15+20+20+20) or (11+15+19+20+20+20 ) =100/109/101/105.
THe only possible case to contain 124 pencils is by considering the case : (24+100 ) = (5, 6,6,7, 11+15+15+19+20+20) = 124 .
Hence box 17 - 20 must contain (20, 29, 31, 33).
Option B: Boxes 17 - 20 contain a total of 108 pencils. Since 29, 31, 33 pencils must be a part of 17 - 20 boxes. The remaining box must contain 108 - (29 +31+33) = 15 pencils. Hence the order is (15, 29, 31, 33).
Option C: Boxes 11- 16 contain a total of 101 defective pencils. This is only possible if the boxes here contain : ( 20, 20, 20, 15, 15, 11) pencils. Hence the box containing 19 pencils must be a part of boxes 17 - 20 and the remaining three contain 29, 31, 33. (19, 29, 31, 33)
Option D : Box number 17 containing more pencils than any box from box number 1- 14. Hence this only possible if Box 15, 16, 17 contains 20 pencils each and 18, 19, 20 contain (29, 31, 33).
Option E : Box 7-16 containing 133 broken pencils :
Boxes (1-6) has 6 boxes with broken pencils which can be included from :
(5, 6, 6, 7, 7, 7, 7, 9, 9, 9). The minimum possible sum of the 6 pencils is : (5+6+6+7) = 24 and the maximum possible sum is (7+9+9+9) = 34.
Boxes 7 - 16 contains all the boxes with broken pencils except one among the boxes with broken pencils among 11 - 20 and hence ;
This can contain : (11+15+15+19+20+20) or (15+15+19+20+20+20) or (11+15+15+20+20+20) or (11+15+19+20+20+20 ) =100/109/101/105.
This has multiple possibilities which include (109 + 24) or (101+32) or (105+28). Hence cannot be uniquely determined
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
