In a class of 150 students, 75 students chose physics, 111 students chose mathematics and 40 students chose chemistry. All students chose at least one of the three subjects and at least one student chose all three subjects. The number of students who chose both physics and chemistry is equal to the number of students who chose both chemistry and mathematics, and this is half the number of students who chose both physics and mathematics. The maximum possible number of students who chose physics but not mathematics, is

Based on the information provided, we can make the following diagram;

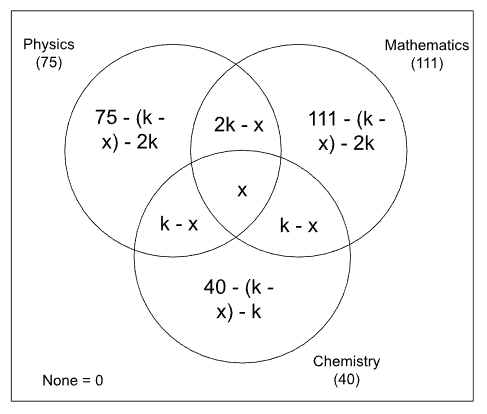
We know that the sum of all entries in the Venn diagram should be $$150$$. Therefore,

$$111+ 75-2k + 40 - (k-x) - k + 0 = 150$$

$$76 = 4k-x$$, where $$x\geq 1$$

We must maximise the number of students who chose Physics but not Mathematics. This number is equal to $$75-2k$$. To maximise this we must minimise $$k$$. 

We have $$4k = 76+x$$ or $$k = 19 + \dfrac{x}{4}$$

Since $$x$$ and $$k$$ are both integers, $$x$$ should be divisible by $$4$$. To minimise $$k$$, we will take the minimum value of $$x$$, which is $$4$$.

Therefore, $$k = 19 + \dfrac{4}{4} = 20$$.

Thus, the maximum possible number of students who chose physics but not mathematics, is $$75-2*20 = 35$$.