Sign in
Please select an account to continue using cracku.in
↓ →
If $$\left( x^{2}+\frac{1}{x^{2}} \right)=25$$ and $$x>0$$, then the value of $$\left( x^{7}+\frac{1}{x^{7}} \right)$$ is
$$\left(x+\dfrac{1}{x}\right)^2 = x^2+\dfrac{1}{x^2} + 2 = 25+2 = 27$$
Therefore, $$\left(x+\dfrac{1}{x}\right) = \sqrt{27} = 3\sqrt{3}$$
Also, $$\left(x+\dfrac{1}{x}\right)^3 = x^3 + \dfrac{1}{x^3} + 3\left(x+\dfrac{1}{x}\right)$$
Therefore, $$x^3 + \dfrac{1}{x^3} = (3\sqrt{3})^3 - 9\sqrt{3} = 72\sqrt{3}$$
Also, $$\left(x^2+\dfrac{1}{x^2}\right)^2 = x^4 + \dfrac{1}{x^4} + 2$$
Therefore, $$x^4 + \dfrac{1}{x^4} = (25)^2 - 2 = 623$$
Lastly, $$\left(x^4+\dfrac{1}{x^4}\right)\left(x^3+\dfrac{1}{x^3}\right) = x^7+\dfrac{1}{x^7} + x + \dfrac{1}{x}$$
Therefore, $$x^7+\dfrac{1}{x^7} = 623*( 72\sqrt{3}) - 3\sqrt{3} = 44853\sqrt{3}$$
Option A is the correct answer.
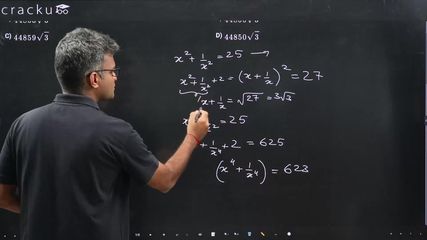
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation