A triangle ABC is formed with AB = AC = 50 cm and BC = 80 cm. Then, the sum of the lengths, in cm, of all three altitudes of the triangle ABC is

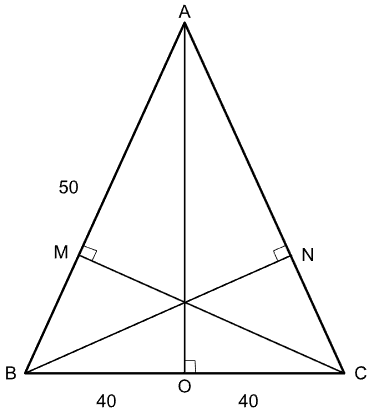
The altitudes $$CM$$ and $$BN$$ will be equal as the triangle $$\triangle ABC$$ is isosceles. 

Further, in $$\triangle AOB$$, using Pythagoras Theorem, we have

$$AO^2 + OB^2 = AB^2$$, therefore, $$AO^2 = 50^2 - 40^2$$

Thus, $$AO^2 = 900$$ or $$AO = 30$$ cm. 

We know that the ratio of altitudes in a triangle is the inverse of the ratio of sides; therefore, the ratio of altitudes of the triangle will be;

$$\dfrac{1}{50} : \dfrac{1}{50} : \dfrac{1}{80} = 8 : 8 : 5$$

Therefore, $$CM = BN = 8x$$ and $$AO = 5x$$.

Since $$5x = 30$$, we have $$x= 6$$, and the sum of altitudes, in centimetres, will be $$8x+8x+5x = 21x = 21*6 = 126$$.