CAT WhatsApp Group
Sign in
Please select an account to continue using cracku.in
↓ →
CAT WhatsApp Group
A circle of diameter 8 inches is inscribed in a triangle ABC where $$\angle ABC = 90^\circ$$. If BC = 10 inches then the area of the triangle in square inches is
Correct Answer: 120
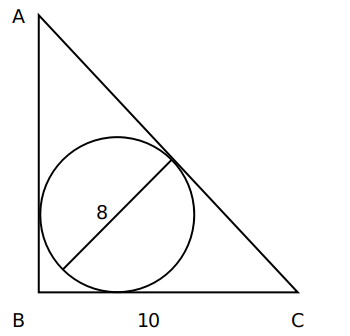
We know that Inradius=$$\frac{\left(Perpendicular+Base-Hypotenuse\right)}{2}$$
$$4=\frac{\left(p+10-h\right)}{2}$$
h-p = 2 or h= p+2.
Now, $$p^2+100\ =\ h^2$$
$$p^2+100\ =\ \left(p+2\right)^2$$
$$p^2+100\ =\ p^2+4p+4$$
4p = 96
p=24.
Hence, Area = $$\frac{1}{2}\times\ 10\times\ 24\ =\ 120$$.
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
